Alexanddros81
- 177
- 4
Homework Statement
Serway Physics Section 2.4 Acceleration
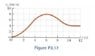
17. Figure P2.17 shows a graph of ##v_x## versus t for the motion of a
motorcyclist as he starts from rest and moves along the road in a straight
line. (a) Find the average acceleration for the time interval t = 0 to t = 6.00 s.
(b) Estimate the time at which the acceleration has its greatest positive
value and the value of the acceleration at that instant. (c) When is the
acceleration zero? (d) Estimate the maximum negative value of the acceleration
and the time at which it occurs.
Homework Equations
The Attempt at a Solution
At part (b) i don't know how to find the value of the acceleration at t = 3s.
Any hints?