How to Determine Final Speeds in a Glancing Collision Problem?

[BrainMan]

Homework Statement

Two identical shuffleboard disks, one orange and the other yellow, are involved in a perfectly elastic glancing collision. The yellow disk is initially at rest and is struck by the orange disk moving with a speed of 4 m/s. After the collision, the orange disk moves along a direction that makes an angle of 30 degrees with its initial direction of motion and the velocity of the yellow disk is perpendicular to that of the orange disk (after the collision). Determine the final speed of each disk.

Homework Equations

The conservation of momentum

The Attempt at a Solution

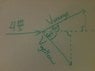
I knew that the initial momentum must be 4 because it is mv. I made both the masses to be one since they are equal to each other to make things simple. Then I tried to find each disks portion of the momentum through trigonometry. At first I treated each of the final velocities paths as the hypotenuses and the value of 4 as one of the sides but I got the wrong answer (see attached image). I eventually found the right answer by messing around with sin and cosine but I still can't visualize the triangles.

 

[Nathanael]

First off let's make sure I made no mistakes; would the answers be $V_{orange}=4m/s$ and $V_{yellow}=\frac{4}{\sqrt{3}} m/s$ ?

I've attatched a drawing of two triangles that I think makes the problem most simple.

Drawing the two triangles that I've attatched and using conservation of momentum you can write two equations:

$V_{orange}cos(30°)+V_{yellow}cos(30°) = 4$

and,

$V_{orange}sin(30°)-V_{yellow}sin(30°) = 0$

Which makes the problem solvable.

 

[BrainMan]

First off let's make sure I made no mistakes; would the answers be $V_{orange}=4m/s$ and $V_{yellow}=\frac{4}{\sqrt{3}} m/s$ ?

I've attatched a drawing of two triangles that I think makes the problem most simple.

Drawing the two triangles that I've attatched and using conservation of momentum you can write two equations:

$V_{orange}cos(30°)+V_{yellow}cos(30°) = 4$

and,

$V_{orange}sin(30°)-V_{yellow}sin(30°) = 0$

Which makes the problem solvable.

The answers would actually be orange = 3.46 m/s and yellow = 2. I found the answer by doing 4 cos 30 and got 3.46 for the orange and 4 cos 60 and got 2 for the yellow. I am not sure how that works based on the diagram I drew. The diagram shows 4 as one of the sides and the unknown velocities as the hypotenuse meaning you would to do 4/ cos 30 and 4/ cos 60 but that makes no sense because you get an answer larger than the original momentum.

 

[CAF123]

The answers would actually be orange = 3.46 m/s and yellow = 2. I found the answer by doing 4 cos 30 and got 3.46 for the orange and 4 cos 60 and got 2 for the yellow. I am not sure how that works based on the diagram I drew. The diagram shows 4 as one of the sides and the unknown velocities as the hypotenuse meaning you would to do 4/ cos 30 and 4/ cos 60 but that makes no sense because you get an answer larger than the original momentum.

Your sketch is correct, but if v_o and v_y are two legs of the triangle with v_i = 4 as the hypotenuse then to get the magnitude of v_o you could split the triangle up into two smaller triangles. But then this changes the length of each of the hypotenuses. See sketch for what I mean.

I think the questioner intended you to use conservation of momentum here. So write equations to conserve momentum in both the horizontal and vertical directions.

 

[Nathanael]

I made a careless mistake in the equations in my last post. Also I obviously made some mistakes while solving them, because I re-solved them, and they do yield the correct answers.

The correct equations would be:

$V_ocos(30°)+V_ycos(60°)=4$

and

$V_osin(30°)-V_ysin(60°)=0$The picture in my last post would still be the same though.Sorry about that.

 

[BrainMan]

I made a careless mistake in the equations in my last post. Also I obviously made some mistakes while solving them, because I re-solved them, and they do yield the correct answers.

The correct equations would be:

$V_ocos(30°)+V_ycos(60°)=4$

and

$V_osin(30°)-V_ysin(60°)=0$


The picture in my last post would still be the same though.


Sorry about that.

Ok I see. Thanks!