Perfectly inelastic collision of two moving and rotating disks

[mattlfang]

Homework Statement

Perfectly inelastic collision of two moving and rotating disk

Relevant Equations

angular momentum, momentum

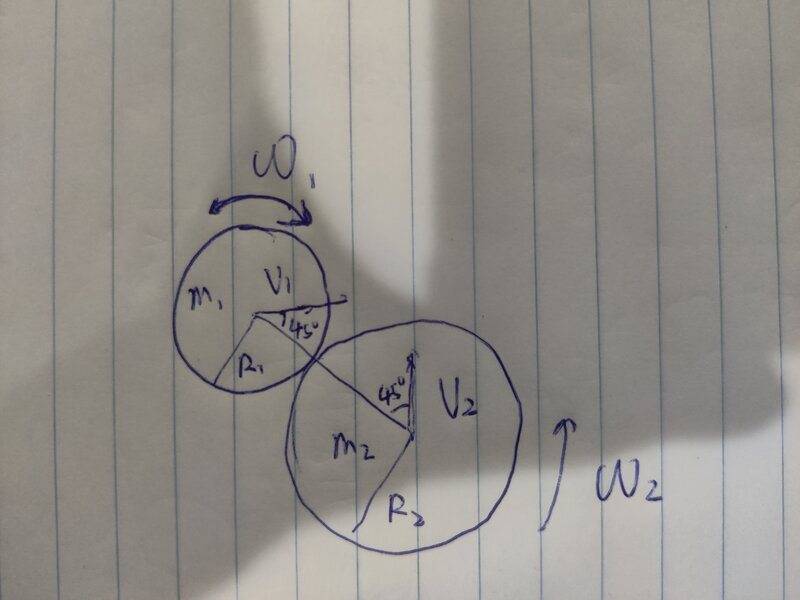
two moving and rotating, uniformly weighted disks perfectly inelastic collide. The disks are rotating in opposite directions (see the diagram) At the moment of their collision, the angles between their velocity and the line connecting their centers are 45 degrees. The velocities are therefore in right angle. We know their angular velocity, their velocities, their radii and their masses. Find the angular velocity after collision.

My thought. Let the center of the mass of the entire system be our reference. We can then ignore the linear momentum and only work on the angular momentum.



The angular momentum of wheel 1 w.r.t center of mass of the whole system is

I₁ ω₁+ m₁ v'₁, where v'₁ is the vertical relative velocity with respect to the center of the mass of the system,

similarly compute angular momentum of wheel 2 w.r.t center of mass of the whole system.

But I got stuck on computing v'₁

Can someone first comment if my above approach is correct, also comment how to find v'₁ ?

 

[PeroK]

Using the CoM frame looks like the way to go. The amalgamated discs are then spinning about their CoM after the collision.

 

[haruspex]

The diagram has information not present in the description. It shows them rotating in opposite directions, and with the velocities at right angles. From the description alone, they could have been rotating the same way and/or moving anti parallel.
Please confirm the diagrammed version.

 

[mattlfang]

The diagram has information not present in the description. It shows them rotating in opposite directions, and with the velocities at right angles. From the description alone, they could have been rotating the same way and/or moving anti parallel.
Please confirm the diagrammed version.

they are rotating in opposite directions yes, but I did mention the velocities are at right angles, let me make that more clear.

 

[haruspex]

Homework Statement:: Perfectly inelastic collision of two moving and rotating disk
Relevant Equations:: angular momentum, momentum

where v'1 is the vertical relative velocity

Do you mean the component of the relative velocity at right angles to the line of centres?

 

[mattlfang]

Do you mean the component of the relative velocity at right angles to the line of centres?

yes, exactly, but it doesn't look easy to express it.

 

[haruspex]

they are rotating in opposite directions yes, but I did mention the velocities are at right angles, let me make that more clear.

No, post #1 says the angles between their velocity and the line connecting their centers are 45 degrees. So the velocities could be at right angles, parallel, or antiparallel.

 

[haruspex]

yes, exactly, but it doesn't look easy to express it.

If you find the velocity relative to the COM, it should be straightforward to take the component at that angle. Is it the first part of that you are unsure about?

 

[mattlfang]

If you find the velocity relative to the COM, it should be straightforward to take the component at that angle. Is it the first part of that you are unsure about?

here is the diagram I drew. I assume wheel A has mass = 1, wheel B has mass = 3, velocity of A is (1,0), and velocity of B is (0,2). Then the velocity of the center of the mass of the system is (0.25, 1.25) vector OD. The velocity relative to the center of the mass of the system is vector AG (0.75, -1.25)

But I struggle to geometrically express its component orthogonal to OA using $m_1, m_2, v_1, v_2$

separately, after two disks collide perfectly inelastically, do they both stop rotating with respect to their own centers, or do they keep rotating, sort of "rolling without slipping," similar to two intermeshing gears?

 

[haruspex]

geometrically express its component orthogonal to OA

You have a component 0.25 in the X direction. What is the component of that normal to OA? Likewise for the Y component, and add them.

sort of "rolling without slipping," similar to two intermeshing gears?

I would say that is what is intended.