nebousuke
- 14
- 0
How to determine the darcy friction factor for irregular cross section tunnels
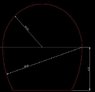
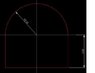
hi, I needed to calculate the f value for tunnels with these cross section area but I am not sure what are method available to calculate these shapes. Two of those cross section areas are already provided as attachments. Any idea where to start? or what sort of methods could I use? And is there any published standards for such calculations for tunnels?
hi, I needed to calculate the f value for tunnels with these cross section area but I am not sure what are method available to calculate these shapes. Two of those cross section areas are already provided as attachments. Any idea where to start? or what sort of methods could I use? And is there any published standards for such calculations for tunnels?
Attachments
Last edited: