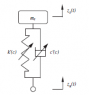
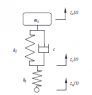
How to find "equivalent stiffness" of the suspension system?

Click For Summary

Discussion Overview

The discussion revolves around finding the equivalent stiffness (k') and damping (c') of a suspension system. Participants explore various methods and approaches related to this problem, including potential energy methods and the treatment of springs and dampers in the system.

Discussion Character

  • Technical explanation
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • One participant expresses a problem in finding the equivalent stiffness and damping of a given equation.
  • Another suggests looking into potential energy methods as a possible approach.
  • A different participant describes a method of combining spring energies, noting that springs in series behave like resistors in parallel, and mentions the potential energy equation V=k(eq)*x^2.
  • There is uncertainty regarding how to incorporate dampers into the stiffness calculation, with one participant suggesting they might be ignored.
  • Another participant proposes writing out the free body diagram (FBD) of the masses and using Laplace transforms to derive transfer functions, although they are unsure of its utility.
  • A participant shares a link to external material related to equivalent viscous damping, indicating it is not covered in their courses.

Areas of Agreement / Disagreement

Participants do not appear to reach a consensus on the best method for finding equivalent stiffness and damping, with multiple competing views and approaches presented throughout the discussion.

Contextual Notes

There are limitations regarding the treatment of dampers in relation to stiffness, and the discussion includes unresolved mathematical steps and assumptions about the system's configuration.

yunias
Messages
1
Reaction score
0
Dude i have a problem to find the equivalent stiffness (k') and damping (c') of this equation ? thank youvery much physics forum
 

Attachments

  • suspension system equivalent.PNG
    suspension system equivalent.PNG
    1.6 KB · Views: 562
  • suspension system.PNG
    suspension system.PNG
    1.6 KB · Views: 590
You may want to look into potential energy methods
 
You add up and combine all of the spring energies taking into account springs in series act like resistors in parallel, then you factor out your x or theta if its rotational isolating the stiffnesses. Potential energy V=k(eq)*x^2

You'll end up with something like V=( terms with k )*x^2
 
Not sure how to factor dampers into a stiffness i feel like they would be ignored

Only other thing i know to do is to write out the fbd of your masses and the middle section on the 2nd image, laplace transform the system equations and get the transfer functions but I'm not sure if that helps you
 

Similar threads

Automotive Calculation of the reduced stiffness of a simple suspension
  • · Replies 3 ·
Replies
3
Views
2K
Automotive Factors Affecting Car Front Suspension: Height, Grip, and Stiffness Explained
  • · Replies 1 ·
Replies
1
Views
2K
How to solve spring mass damper system manually?
  • · Replies 16 ·
Replies
16
Views
4K
Help me understand how bolts take less load than members
  • · Replies 5 ·
Replies
5
Views
2K
How to Motorize a Stiff TV Mount with Swivel Arm Joints?
  • · Replies 9 ·
Replies
9
Views
2K
Can adjustable torsion springs be used in suspension systems?
  • · Replies 16 ·
Replies
16
Views
7K
Automotive Stiffness and dumping coeficients of a VW Golf
  • · Replies 3 ·
Replies
3
Views
4K
Structure adding rotational stiffness to a plate
  • · Replies 15 ·
Replies
15
Views
2K
Differential Equations and Damper Curves
  • · Replies 3 ·
Replies
3
Views
2K
Engineering Total Lateral Stiffness from Stiffness Matrix
  • · Replies 0 ·
Replies
0
Views
2K