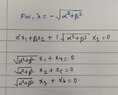Discussion Overview
The discussion revolves around finding generalized eigenvectors in the context of a matrix ordinary differential equation (ODE). Participants explore the relationship between algebraic and geometric multiplicities of eigenvalues, the calculation of eigenvectors, and the implications of Jordan normal forms.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Alwar seeks assistance in finding generalized eigenvectors using the algorithm (A-λI)w=v, expressing difficulty in obtaining the eigenvector matrix M.
- Some participants express confusion regarding the eigenvalues, noting discrepancies between the stated eigenvalues and those found in the Jordan normal form.
- There are requests for clarification on the specific problems encountered in calculating eigenvectors, with some participants questioning whether generalized eigenvectors can be set aside initially.
- Participants discuss the implications of degenerate eigenvalues and the freedom in choosing eigenvectors, suggesting that multiple orthogonal eigenvectors can be selected.
- One participant describes a method for finding a specific eigenvector that allows for the construction of a Jordan chain, emphasizing that it is not a random vector but one that satisfies the system.
- There are mentions of typos in the original attachments, particularly regarding the eigenvalues and the Jordan matrix.
- Vela shares a method of finding eigenvectors through augmented matrices and row reduction, but later states that they cannot provide their calculations as they were done in Mathematica without saving the notebook.
Areas of Agreement / Disagreement
Participants express confusion and disagreement regarding the eigenvalues and the calculation of eigenvectors. There is no consensus on the correct interpretation of the eigenvalues or the method for finding the generalized eigenvectors, indicating multiple competing views remain.
Contextual Notes
Limitations include potential typos in the original problem statement, unresolved mathematical steps in finding eigenvectors, and the dependence on specific definitions of eigenvalues and eigenvectors in the context of the discussion.