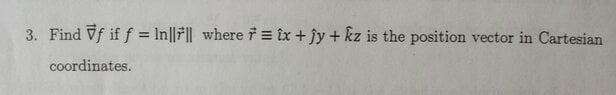SUMMARY
The gradient of the function f = ln|r| is calculated using the chain rule, resulting in the expression ∇f = (x,y,z)/√(x²+y²+z²) = r̂/r². The discussion clarifies that the gradient of 1/r is given by ∇(1/r) = -r/r³. Participants emphasized the importance of correctly applying partial derivatives and the chain rule in vector calculus to derive these gradients accurately.
PREREQUISITES
- Understanding of vector calculus concepts, particularly gradients
- Familiarity with the chain rule in differentiation
- Knowledge of partial derivatives and their notation
- Basic understanding of the Euclidean norm in three-dimensional space
NEXT STEPS
- Study the application of the chain rule in vector calculus
- Learn about the properties and applications of gradients in physics and engineering
- Explore the derivation of gradients for other scalar fields
- Investigate the implications of gradients in optimization problems
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are looking to deepen their understanding of vector calculus and its applications in real-world scenarios.