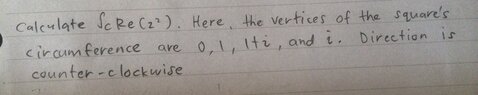aruwin
- 204
- 0
Hello.
I am stuck at the third point, that is from 1+i to i. I asked someone to show me his answer but that part of his is different from mine. Is his solution correct?
Here it is:
(i) z = 0 to 1 via z(t) = t with t in [0, 1]:
∫c1 Re(z^2) dz
= ∫(t = 0 to 1) Re(t^2) * 1 dt
= ∫(t = 0 to 1) t^2 dt
= 1/3.
(ii) z = 1 to 1+i via z(t) = 1+it with t in [0, 1]:
∫c2 Re(z^2) dz
= ∫(t = 0 to 1) Re((1 + it)^2) * (i dt)
= ∫(t = 0 to 1) (1 - t^2) * i dt
= i(t - t^3/3) {for t = 0 to 1}
= 2i/3.
(iii) z = 1+i to i via z(t) = t+i with t in [0, 1] and opposite orientation:
∫c3 Re(z^2) dz
= -∫(t = 0 to 1) Re((t+i)^2) * 1 dt
= -∫(t = 0 to 1) (t^2 - 1) dt
= -(t^3/3 - t) {for t = 0 to 1}
= 2/3.
(iv) z = i to 0 via z(t) = it with t in [0, 1] and opposite orientation:
∫c4 Re(z^2) dz
= -∫(t = 0 to 1) Re((it)^2) * i dt
= -∫(t = 0 to 1) -it^2 dt
= i/3.
So, ∫c Re(z^2) dz = 1/3 + 2i/3 + 2/3 + i/3 = 1 + i.
I am stuck at the third point, that is from 1+i to i. I asked someone to show me his answer but that part of his is different from mine. Is his solution correct?
Here it is:
(i) z = 0 to 1 via z(t) = t with t in [0, 1]:
∫c1 Re(z^2) dz
= ∫(t = 0 to 1) Re(t^2) * 1 dt
= ∫(t = 0 to 1) t^2 dt
= 1/3.
(ii) z = 1 to 1+i via z(t) = 1+it with t in [0, 1]:
∫c2 Re(z^2) dz
= ∫(t = 0 to 1) Re((1 + it)^2) * (i dt)
= ∫(t = 0 to 1) (1 - t^2) * i dt
= i(t - t^3/3) {for t = 0 to 1}
= 2i/3.
(iii) z = 1+i to i via z(t) = t+i with t in [0, 1] and opposite orientation:
∫c3 Re(z^2) dz
= -∫(t = 0 to 1) Re((t+i)^2) * 1 dt
= -∫(t = 0 to 1) (t^2 - 1) dt
= -(t^3/3 - t) {for t = 0 to 1}
= 2/3.
(iv) z = i to 0 via z(t) = it with t in [0, 1] and opposite orientation:
∫c4 Re(z^2) dz
= -∫(t = 0 to 1) Re((it)^2) * i dt
= -∫(t = 0 to 1) -it^2 dt
= i/3.
So, ∫c Re(z^2) dz = 1/3 + 2i/3 + 2/3 + i/3 = 1 + i.
Attachments
Last edited: