How to find the net acceleration?

[navneet9431]

Homework Statement

This is the question(16) I am going to talk about.

Homework Equations

Acceleration=Force/Mass

The Attempt at a Solution

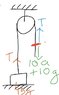
I drew a Free Body Diagram for this question.Here,The red mark shows the point on the rope at which the monkey applies the force(10a).
So for the block to move up T<10a+10g and T>15g.
So,At the red mark
10(a+g)-T=10*a (Net Acceleration)...(i)
And for the block,
T-15g=15*a (Net Acceleration)....(ii)
So I have successfully find two equation.
What should I do next to get the final answer?

I will be thankful for help!

 

[andrewkirk]

It is usual in problems like this to ignore the acceleration of the block that is needed to raise it a couple of millimetres off the floor. As long as the tension in the rope is greater than the weight of the block, by however small a margin, the block will raise off the floor, if we ignore friction. So we can effectively regard the block as being stationary, and so the rope is also stationary, while the monkey scrambles up the rope.

So the problem becomes:

(1) what tension must the rope have in it to support the stationary block off the ground but not accelerate it upwards other than negligibly? and
(2) how fast will the monkey accelerate upwards, climbing the rope, if the rope is pulling up on him by that tension (and he is pulling back down on the rope by the same tension)?

 

[navneet9431]

How could you say that the monkey is pulling back on the rope by the same tension?

It is usual in problems like this to ignore the acceleration of the block that is needed to raise it a couple of millimetres off the floor. As long as the tension in the rope is greater than the weight of the block, by however small a margin, the block will raise off the floor, if we ignore friction. So we can effectively regard the block as being stationary, and so the rope is also stationary, while the monkey scrambles up the rope.

So the problem becomes:

(1) what tension must the rope have in it to support the stationary block off the ground but not accelerate it upwards other than negligibly? and
(2) how fast will the monkey accelerate upwards, climbing the rope, if the rope is pulling up on him by that tension (and he is pulling back down on the rope by the same tension)?

 

[Delta2]

Equation (ii) seems correct. Inequality T>15g is correct.

But equation (i) and inequality T<10a+10g are incorrect. The force that the monkey applies to the rope is not 10a it is -10(a+g)=-T. To prove this make a FBD for the monkey and use Newton's second law. Also use Newton's 3rd law to prove that the force that the monkey applies to the rope equals -T.

 

[Delta2]

How could you say that the monkey is pulling back on the rope by the same tension?

This is Newton's 3rd Law: The rope applies to the monkey force T, hence the monkey applies to the rope force -T.

 

[haruspex]

As @Delta² notes, this

T<10a+10g

should really be an equality. But what you had here:

T<10a+10g and T>15g.

was enough to solve the problem. Just combine them to eliminate T.