kindejj
- 3
- 0
Hi all,
I apologize now at how elementary this is, but I have been all over google and I cannot get a straight answer. My question seems to me be to be quite easy. Maybe I am over simplifying it. Anyways, any help is much appreciated. Btw, it's been 15 years since my last physics class, so be patient please!
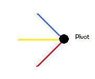
If I have 3 levers attached to the same pivot, one at 45 degrees, one at 0 degrees at one at -45 degrees, each lever being 1 meter long, and a 100 gram mass at the end of each. How do I go about measuring the force that each lever is applying to the pivot?
Thanks in advance. See attachment for example.
I apologize now at how elementary this is, but I have been all over google and I cannot get a straight answer. My question seems to me be to be quite easy. Maybe I am over simplifying it. Anyways, any help is much appreciated. Btw, it's been 15 years since my last physics class, so be patient please!
If I have 3 levers attached to the same pivot, one at 45 degrees, one at 0 degrees at one at -45 degrees, each lever being 1 meter long, and a 100 gram mass at the end of each. How do I go about measuring the force that each lever is applying to the pivot?
Thanks in advance. See attachment for example.
 … they aren't levers!
… they aren't levers!