- #1
powdernose
- 12
- 0
I am not a student btw,
this is seeking extra knowledge regarding a hobby of mine, and it has been too long since I've tried to solve a physics problem.
1. Homework Statement
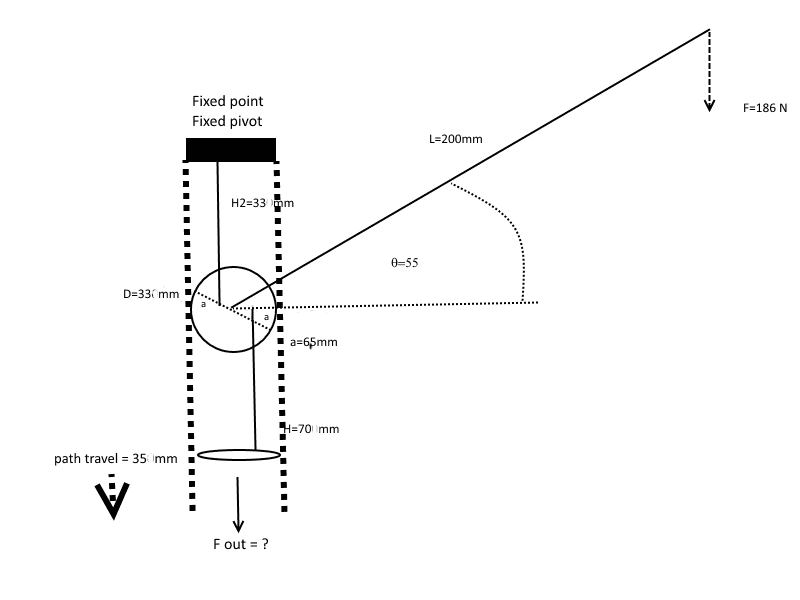
I have the above system in which Lever L (200mm) applies force to a crank D (diameter 33mm), which has a reverse motion linkage system with rod H2 (33mm) attached to a fixed object, and rod H (70mm) attached to a cylinder which it pushes through a path with a total travel of 35mm ( the crank moves through the path too). The lever L has a range of motion from perpendicular through to 45 degrees below the horizontal. I've chosen θ 55 degrees, because that is essentially where resistance starts, and where the pivot points of H and H2 on the crank are at horizontal.
H and H2 pivots are a=6.5mm from the perimeter of the crank, so they are at radius r=10mm.
My diagram is a bit poor as it doesn't show that H and H2 have pivots on their ends, so their angle changes throughout the motion.
I'm looking to calculate the force exerted by H2 on the bottom cylinder,
or rather the mechanical advantage throughout the range of motion.
Torque
T = F * L * sin(90-theta)
Pythagoreum
r^2 +H^2 = X^2
Crank position
x = r.cos A + sqrt{H^2 - r^2\sin^2 A}
Constant
Angle A = θ + 45 degrees
I can calculate the torque on the crank with a perpendicular force of 186 N applied as pictured at θ 55 degrees,
to T= 21.34 Nm.
And at this moment the distance X perpendicular from the crank to the bottom cylinder = 70.7mm
but what is the perpendicular force applied on the cylinder by H at this moment?
How does one calculate mechanical advantage?
I've looked through slider crank materials, but it is always with regard to angular velocity,
I'm only interested in the perpendicular force applied on the bottom cylinder throughout the motion in relation to the perpendicular force applied to the Lever H.
Is it a problem of net torque? with the counter torque applied at a lever of the offset radius of H 10mm?thanks for the help
this is seeking extra knowledge regarding a hobby of mine, and it has been too long since I've tried to solve a physics problem.
1. Homework Statement
I have the above system in which Lever L (200mm) applies force to a crank D (diameter 33mm), which has a reverse motion linkage system with rod H2 (33mm) attached to a fixed object, and rod H (70mm) attached to a cylinder which it pushes through a path with a total travel of 35mm ( the crank moves through the path too). The lever L has a range of motion from perpendicular through to 45 degrees below the horizontal. I've chosen θ 55 degrees, because that is essentially where resistance starts, and where the pivot points of H and H2 on the crank are at horizontal.
H and H2 pivots are a=6.5mm from the perimeter of the crank, so they are at radius r=10mm.
My diagram is a bit poor as it doesn't show that H and H2 have pivots on their ends, so their angle changes throughout the motion.
I'm looking to calculate the force exerted by H2 on the bottom cylinder,
or rather the mechanical advantage throughout the range of motion.
Homework Equations
Torque
T = F * L * sin(90-theta)
Pythagoreum
r^2 +H^2 = X^2
Crank position
x = r.cos A + sqrt{H^2 - r^2\sin^2 A}
Constant
Angle A = θ + 45 degrees
The Attempt at a Solution
I can calculate the torque on the crank with a perpendicular force of 186 N applied as pictured at θ 55 degrees,
to T= 21.34 Nm.
And at this moment the distance X perpendicular from the crank to the bottom cylinder = 70.7mm
but what is the perpendicular force applied on the cylinder by H at this moment?
How does one calculate mechanical advantage?
I've looked through slider crank materials, but it is always with regard to angular velocity,
I'm only interested in the perpendicular force applied on the bottom cylinder throughout the motion in relation to the perpendicular force applied to the Lever H.
Is it a problem of net torque? with the counter torque applied at a lever of the offset radius of H 10mm?thanks for the help
Attachments
Last edited by a moderator: