abcs22
- 11
- 0
1. Homework Statement prove the following statement:
Hello, can someone help me prove this statement
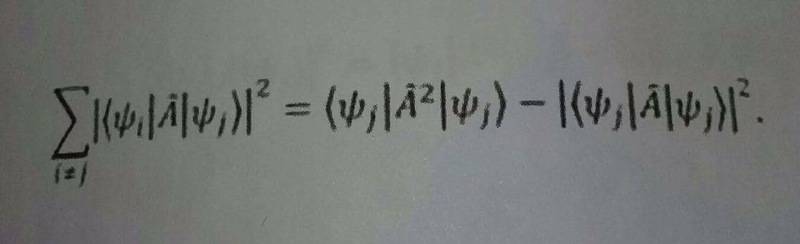
A is hermitian and {|Ψi>} is a full set of functions
Σ<r|A|s> <s|B|c>[/B]
Since the right term of the equation reminds of the standard deviation, I tried using its definition but it didn't yield any results. Also, I tried to use the hermicity of the operator A to get the complete set but after that I got stuck.
Hello, can someone help me prove this statement
A is hermitian and {|Ψi>} is a full set of functions
Homework Equations
Σ<r|A|s> <s|B|c>[/B]
The Attempt at a Solution
Since the right term of the equation reminds of the standard deviation, I tried using its definition but it didn't yield any results. Also, I tried to use the hermicity of the operator A to get the complete set but after that I got stuck.