Md. Abde Mannaf
- 20
- 1
Homework Statement
Homework Equations
The Attempt at a Solution
here is i am still stuck.
The discussion revolves around the application of the Leibniz rule in calculus, particularly in the context of evaluating integrals that involve variable limits and parameters. Participants are attempting to solve a specific integral problem that appears to involve trigonometric functions and possibly some typographical errors in the problem statement.
The discussion is ongoing, with various participants sharing their thoughts and approaches. Some have provided links to resources for further exploration, while others are seeking more guidance on how to proceed with the integral. There is no clear consensus on a single method or solution at this point.
Participants note that the limits of the integral are constant, which affects the application of the Leibniz rule. There is also mention of using computational tools like Wolfram Alpha to assist with the problem.
Don't use substitution, use Leibniz rule with α as the second variable.
Md. Abde Mannaf said:i know the Leibniz's rule. i solve many mathematical term . bt i cann't solve this math with Leibniz rule. i am still stuck
here. here limit is constant so 2nd and 3rd term will be zero.
See this, example 3.Zondrina said:if you are intending to use Leibniz rule. I for one have never seen an In\text{In} function before.
You can even cheat :) using wolframalpha.com.Md. Abde Mannaf said:Homework Statement
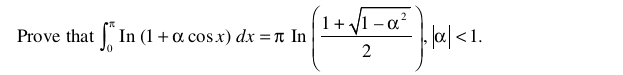
Homework Equations
The Attempt at a Solution
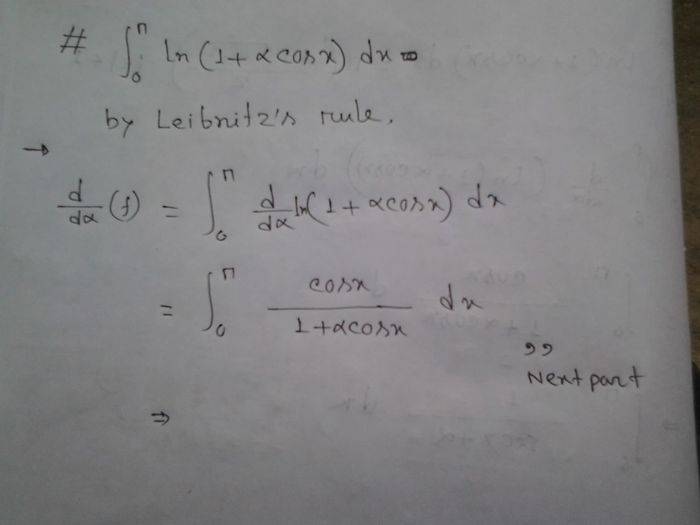
here is i am still stuck.
Zondrina said:I believe there are quite a few typos in the problem statement if you are intending to use Leibniz rule. I for one have never seen an ##\text{In}## function before.
The Leibniz rule in one dimension would be:
$$\frac{d}{dx} \int_{a(x)}^{b(x)} f(t) dt = f(b(x)) b'(x) - f(a(x)) a'(x)$$
EDIT: It would be more appropriate to call this the fundamental theorem.
Does no one read my posts :-)ehild said:You can even cheat :) using wolframalpha.com.
You can write your integral for ##f'(\alpha)## as ##\int_0^{\pi/2} + \int_{\pi/2}^{\pi}##, then change variables to ##x \leftarrow \pi -x## in the second integral, to getMd. Abde Mannaf said:i could not solve this math above analysis . i am trying to my best. but i am fail every time. and again try...
please see this and give me more idea to solve
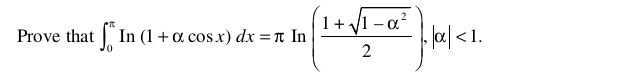
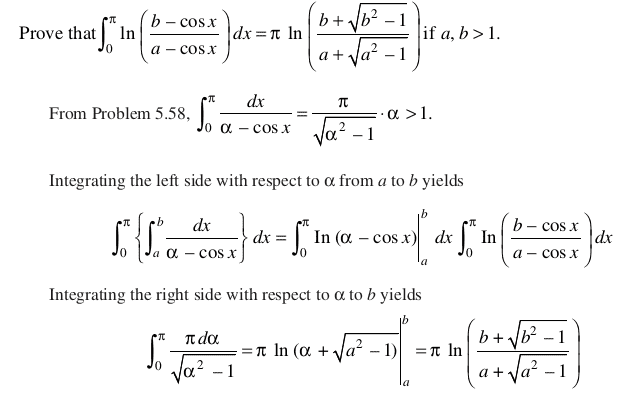
##\int \frac{1}{1+\alpha cos(x)} dx## is not that nasty.certainly said:Now let's do that daunting looking integral. Like I said before, this is a good problem.
First write ##\int_0^{\pi} \frac{1}{\alpha}-\frac{1}{(\alpha)(1+\alpha cos(x))} dx## for the original integral.
However ##\int \frac{1}{1+\alpha cos(x)} dx## itself is not nice, in-fact it's pretty nasty.
Yeah, your right. I didn't actually do the integral, I only saw the answer and thought, this might take some time.ehild said:##\int \frac{1}{1+\alpha cos(x)} dx## is not that nasty.
Use the identity ##\cos(x)=\frac{1-\tan^2(x/2)}{1+\tan^2(x/2)}##. Substitute u=tan(x/2), x=2arctan(u), ##dx=\frac{2}{1+u^2}du##. The integration limits become 0-->infinite.