How to understand Proton Structure-function (pdf)

[edfink234]

I don't understand the attached image, which shows the structure-function of the proton, for the cases of
1. point-like particle
2. 3 non-interacting quarks
3. 3 quarks interacting via gluons
4. valence and sea quarks interacting via gluons

Can someone please explain this to me? I would greatly appreciate it.

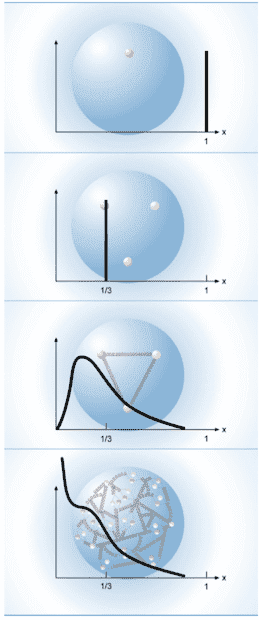
The vertical axis is the structure-function for a fixed Q^2, the horizontal axis is the Bjorken x.

 

[Orodruin]

What have you read about the subject? Which part do you have difficulty understanding?

The best place to start is a textbook. You are basically asking us to write textbook material here.

 

[mathman]

My very limited knowledge: 4 is complete description.

 

[vanhees71]

The four images depict descriptions on different scales of resolution the partonic structure of the proton. It's investigated in scattering of electrons on a proton. The higher the scattering energy is the more "microscopic details" of the scattering object is revealed. At low energies one can well described the scattering as Coulomb scattering, i.e., describing the proton by a point-particle Coulomb potential. At somewhat higher energies one finds that there is a "form factor", i.e, a deviation from a pure point-particle Coulomb potential indicating that the Proton is an extended object with a corresponding charge distribution. Going even higher in energy, one finds a cross section that is explained by the assumption that the proton consists of 3 point-like constituent quarks. Going even higher reveals that there are also sea quarks and antiquarks. From QCD it's also clear that there must be gluon fields too, and in fact QCD has been discovered from the investigation of this deep inelastic scattering of electrons and protons (starting with the discovery of Bjorken scaling at SLAC and Feynman's explanation in terms of the "parton model").

 

[ohwilleke]

Part of the problem is that the two dimensional chart is a depiction of a data set that is more than two dimensional. Each chart depicts probabilities for only one particular kind of parton. For example, what is the probability that if we smash a proton that a muon will come out. But this is only a tiny part of the total picture of what is going on inside a proton and could come out of one if you "poke" it.

To capture the full structure of a proton, you need something more like the images that appear behind the charts (ideally in three dimensions, although symmetry considerations make the two dimensional images less bad than they would be otherwise), that depict every possible kind of particle that could be produced, all at once.

Also, just to be fussy, if you are really going to do an image like the third one correctly, the lines that depict gluons between the valence quarks would curve towards the center, because they have found that gluons are concentrated in the middle of a proton rather than closer to its edges.