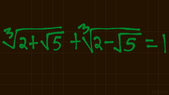SUMMARY
The discussion focuses on verifying radical equations algebraically, specifically addressing the method to confirm that both sides of the equation are equal without the use of a calculator. Participants emphasize the importance of manipulating the equation through algebraic techniques such as squaring both sides and isolating the radical. The conversation also references a previous question on the Math Help Boards, highlighting the value of archived discussions for educational purposes.
PREREQUISITES
- Understanding of algebraic manipulation techniques
- Familiarity with radical expressions
- Knowledge of squaring both sides of an equation
- Ability to isolate variables in equations
NEXT STEPS
- Study the process of solving radical equations in detail
- Learn about common pitfalls in algebraic verification
- Explore examples of radical equations and their solutions
- Investigate the implications of extraneous solutions in radical equations
USEFUL FOR
Students, educators, and anyone interested in mastering algebraic techniques for solving and verifying radical equations.