Sam Donovan
- 11
- 0
Member advised to do some research before posting
Specifically:
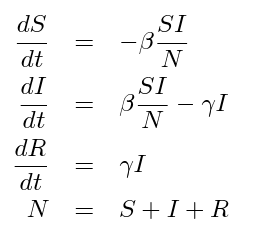
The discussion centers on the calculation of differential equations for SIR (Susceptible, Infected, Recovered) models, emphasizing their reliance on parameters such as β (transmission rate), γ (recovery rate), and initial conditions. The validity of these models is determined through empirical data comparisons rather than formal mathematical proofs. Key references include the original paper by Reed and Frost and relevant Wikipedia entries that provide foundational knowledge and context for understanding these models in infectious disease modeling.
PREREQUISITESResearchers, epidemiologists, and students interested in mathematical modeling of infectious diseases, particularly those focusing on SIR models and their applications in real-world scenarios.
Thank you! Do you think there any sites or wiki articles with the math proof for these equations?fresh_42 said:Here's the related Wikipedia entry on the issue:
https://en.wikipedia.org/wiki/Mathematical_modelling_of_infectious_disease