- 1,242
- 1,051
I would like to propose an olympic (as it seems to me) level problem.
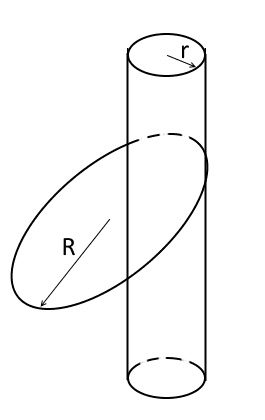
There is a vertical pillar of radius r and a thin hoop of mass m and radius R( R>r).
The hoop putted on the pillar rotates such that the center of the hoop describes a circle in horizontal plan and the velocity of the center remains constant in its absolute value. The is no slipping between the hoop and the pillar. The hoop does not slides down being undergone with the gravity.
Show that if R>4r/3 then, for some suitable values of the velocity and the friction coefficient between the hoop and the pillar, the described above motion is possible. And if R<4r/3 then independently on the friction and the velocity such a motion does not exist.
What do you think about the problem? I do not ask a solution :) I just expect teaching professional comments
There is a vertical pillar of radius r and a thin hoop of mass m and radius R( R>r).
The hoop putted on the pillar rotates such that the center of the hoop describes a circle in horizontal plan and the velocity of the center remains constant in its absolute value. The is no slipping between the hoop and the pillar. The hoop does not slides down being undergone with the gravity.
Show that if R>4r/3 then, for some suitable values of the velocity and the friction coefficient between the hoop and the pillar, the described above motion is possible. And if R<4r/3 then independently on the friction and the velocity such a motion does not exist.
What do you think about the problem? I do not ask a solution :) I just expect teaching professional comments