HW Question regarding double-slit interference

[SoundsofPhysics]

A Homework Question about double-slit interference reads as such:
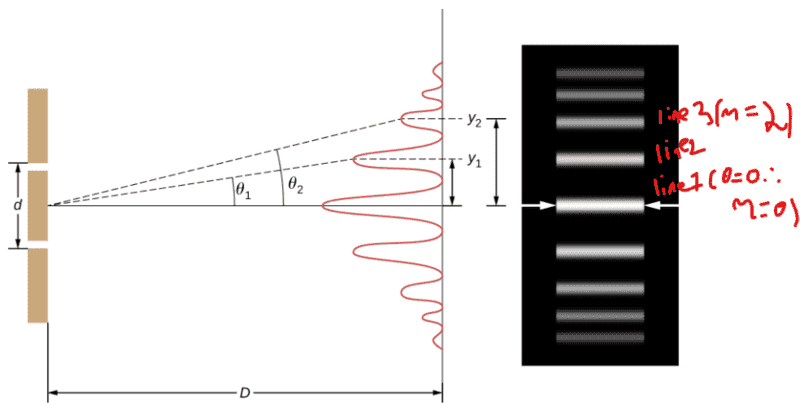
"Finding a Wavelength from an Interference Pattern
Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of 10.95° relative to the incident beam. What is the wavelength of the light?"
I used the equation:
d* sin *(theta) = m * lambda
0.01 * sin(10.95) = 2 * lambda
lambda = 949nm
The difference they did is using m = 3. But shouldn't the third line on the screen have m = 2 because the first line has m = 0 (It is the center, so theta = 0 and m must equal zero). Am thinking about it wrong? If so, how?

 

[kuruman]

The pattern is symmetric above and below the central line. The m-values, which denote the order of the maxima, are like an integer number line. In the photo you have zero at the origin from where you start counting, i.e. the central maximum is line "0". Then the next numbers are +1 above and -1 below for the first maxima which must occur at the same angle θ₁ above and below the central maximum. Thus, there is only one line at m = 0, θ = 0 , two lines at m = ± 1 θ = ±θ₁, and so on.

It looks like you made the same counting mistake that people made centuries ago when they omitted "year zero." According to https://en.wikipedia.org/wiki/Year_zero, "A year zero does not exist in the Anno Domini (AD) calendar year system commonly used to number years in the Gregorian calendar (nor in its predecessor, the Julian calendar); in this system, the year 1 BC is followed directly by year AD 1."

 

[Mister T]

Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of [...]

The question is very poorly worded. If they intended for the value of $m$ to be $3$ they should have stated that it's the third line from the central maximum. I agree with your logic: The phrase "third bright line" can be interpreted in the way you have and that if so then $m=2$.

 

[kuruman]

The question is very poorly worded. If they intended for the value of $m$ to be $3$ they should have stated that it's the third line from the central maximum. I agree with your logic: The phrase "third bright line" can be interpreted in the way you have and that if so then $m=2$.

My logic says that if one counts starting at either end of the pattern, "line 1" would be the bottommost line or topmost line, depending on whether counts bottom to top or top to bottom. If one wants to start counting from the middle of the array, one does not start at one but at zero. The implication is that one direction is positive and the other direction is negative with zero at the boundary. Also, it makes more sense (at least to me) to say that the central line is the zeroth line and start there because it is unique in the pattern; it is the only line which is formed by equal path lengths. All the other lines come in pairs at equal angles.

Also, according to your scheme, the label of the first line above the central line is "2" in which case the label of the first line below the central line must be "0". The next two lines at equal angles would be "3" and "-1". If this labeling scheme makes sense to you, try teaching it to a class of undergraduates.

I agree with you that the problem is not very clear. A well written problem might say something like "the third line from the central maximum". However, the convention of labeling the central maximum "0" to match the path length difference from the slits to it is common and therefore not mentioned explicitly by some authors. This convention allows the line count number, the integer $m$ in the equation, and the path length difference in units of wavelength to be one and the same.

 

[haruspex]

The pattern is symmetric above and below the central line. The m-values, which denote the order of the maxima, are like an integer number line. In the photo you have zero at the origin from where you start counting, i.e. the central maximum is line "0". Then the next numbers are +1 above and -1 below for the first maxima which must occur at the same angle θ₁ above and below the central maximum. Thus, there is only one line at m = 0, θ = 0 , two lines at m = ± 1 θ = ±θ₁, and so on.

It looks like you made the same counting mistake that people made centuries ago when they omitted "year zero." According to https://en.wikipedia.org/wiki/Year_zero, "A year zero does not exist in the Anno Domini (AD) calendar year system commonly used to number years in the Gregorian calendar (nor in its predecessor, the Julian calendar); in this system, the year 1 BC is followed directly by year AD 1."

All true, but does not answer the question of how "third bright line" should be interpreted. "Third brightest line" would clearly be $m=\pm 2$.

 

[vanhees71]

Indeed, it's a very badly formulated question. From the information that the light comes from a He-Ne laser it's clear that they meant ##m=3#, because the usual visible-light line is at 633 nm.

 

[Mister T]

If one wants to start counting from the middle of the array, one does not start at one but at zero.

Certainly the value of $m$ is zero at the middle of the array. But the first counting number is $1$, not $0$.

 

[kuruman]

All true, but does not answer the question of how "third bright line" should be interpreted. "Third brightest line" would clearly be $m=\pm 2$.

To me it's clear that the "third bright line" is $m=\pm 3$ but I will stop here. I think that this argument is analogous to a European and an American arguing whether one has to climb two or three flights of stairs to get to the third floor of a building. The answer is clear to each one of them until they agree to disagree.

 

[Mister T]

I think that this argument is analogous to a European and an American arguing whether one has to climb two or three flights of stairs to get to the third floor of a building. The answer is clear to each one of them until they agree to disagree.

What they disagree about must be whether or not the ground floor is the first floor or the zeroth floor. It's not about whether or not you start counting at zero.