Settho
- 4
- 0
OP warned about not using the homework template
If A and B are Hermitian operators is (i A + B ) a Hermitian operator?
(Hint: use the definition of hermiticity used in the vector space where the elements are quadratic integrable functions)
I know an operator is Hermitian if:
- the eigenvalues are real
- the eigenfunction is orthonormal
- the eigenfunctions form a complete basis set.
I know how to prove if A + B is a Hermitian operator, but because of the i in front of A I still am a little bit confused.
So I know to prove if the eigenvalues are real. You have to use these integrals first and prove both sides are the same so that λ = λ*
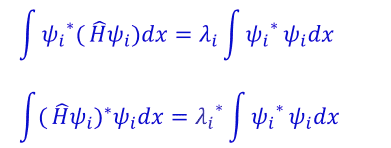
So I did this:
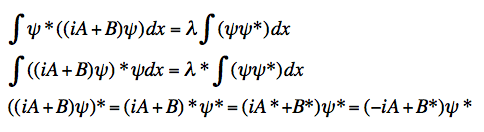
I have doubts about the last one, because I think that is now how it is suppose to go, but I don't know. And then I thought because both sides aren't the same the eigenvalues aren't real and it isn't Hermitian.
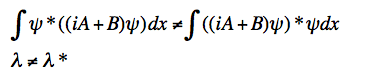
Is this correct? If it isn't how am I suppose to handle this problem?
(Hint: use the definition of hermiticity used in the vector space where the elements are quadratic integrable functions)
I know an operator is Hermitian if:
- the eigenvalues are real
- the eigenfunction is orthonormal
- the eigenfunctions form a complete basis set.
I know how to prove if A + B is a Hermitian operator, but because of the i in front of A I still am a little bit confused.
So I know to prove if the eigenvalues are real. You have to use these integrals first and prove both sides are the same so that λ = λ*
So I did this:
I have doubts about the last one, because I think that is now how it is suppose to go, but I don't know. And then I thought because both sides aren't the same the eigenvalues aren't real and it isn't Hermitian.
Is this correct? If it isn't how am I suppose to handle this problem?