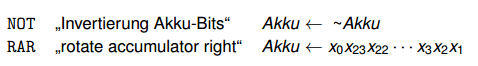Implement MIMA Function EQL adr - Wondering

[mathmari]

Hey!

We have that MIMA (Neumann MInimal MAchine) has the following commands:

LCD const   :  Load constant 
LDV adr      :  Load value from address 
LDIV adr     :  Load value indirect from address 
STV adr      :  Set value at address 
STIV adr     :  Set value indirect at address

View attachment 6290

NOT            :   Inverse of the constant-bits   
RAR            :   Rotate accumulator right

View attachment 6291

ADD adr      :   Addition 
AND adr      :   bitwise AND 
OR  adr       :   bitwise OR 
XOR adr      :   bitwise exclusive OR

View attachment 6292

JMP  adr      :   Jump 
JMN adr       :   Jump if negative

I want to write a MIMA program that takes the value $2^{23}-24=8.388.584$ to the memory $y$.
We have to take attention at the number of the bits, that we need for the representation of the number in two's complement.

How do exactly do we make the representation? (Wondering)

The other part is the following, or not?

LDC  const 
STIV  y

Then I want to implement the Mima-command EQL adr (equal?) with the other Mima-commands.

We have that for that command it holds the following: $$\text{Accu} \leftarrow \left\{\begin{matrix}
-1 , &\text{ Accu }=M(adr)\\
0 , &\text{otherwise}
\end{matrix}\right.$$

I have done the following:
My idea is to compute -M(adr) and then to add it to Accu, and then to check if it i <0.
And then to compute the inverse of the result and check if it is <0.
Is it correct? (Wondering)

LCD const 
LDV adr 
NOT 
STV adr 
ADD adr 
STV adr 
JMN x 
LDC -1 
JMP z 
x: LCD 0 
z: NOT 
   JMN m 
   LDC -1 
   JMP n 
   m: LCD 0 
   n: STV adr

Is the implementation correct? Could I improve something? (Wondering)

 

[mathmari]

We have also the following information about the bits:
Address: 20 Bit and Values: 24 Bit

 

[mathmari]

About the representation of the number in two's complement, I have done the following:

We have that $2^{n+1}=2\cdot 2^n=2^n+2^n$.

So, $$2^1=2^0+2^0=1+1 \\ 2^2=2^1+2^1=(1+1)+(1+1) \\ 2^3=2^2+2^2=[(1+1)+(1+1)]+[(1+1)+(1+1)] \\ \text{etc} $$

And we have that $24=2^3\cdot 3=2^3+2^3+2^3$.

We initialize the memory cell $y$ with $1$ and we repeat $23$ times to add the value of $y$ by itself and the result we put it at $y$.

Then we have to subtract three times $2^3$.

How do we do this? Do we have to compute again the $2^3$'s, then compute the inverse and add it to the value that is at $y$ ?

But where do we do these operations? To calculate $2^3$ as above, we have to save the results at each step, or not? But where? Do we consider an other memory cell, say $a$, for that? (Wondering)

Let $x$ be the memory cell where the representation of $23$ in two's complement is, and let $z$ be the memory cell where the representation of $3$ in two's complement is.

I wrote the following code (about the part of $2^3$ I computed it in the way we compute $2^{23}$ and I subtracted it three times from $y$):

            LCD 1 
            STV y 
while1:     LDC 0 
            NOT 
            ADD x 
            STV x 
            JMN end1 
            LDV y 
            ADD y 
            STV y 
           JMP while1 
end1:       LDC 1 
            STV a 
while2:     LDC 0 
            NOT 
            ADD z 
            STV  z
            JMN end2 
            LDV a 
            ADD a 
            STV a 
            JMP while2 
end2:       LDV a 
            NOT 
            ADD y 
            LDV a 
            NOT 
            ADD y 
            LDV a 
            NOT 
            ADD y 
            HALT

Is this correct? (Wondering)