Ineedhelpwithphysics
- 43
- 7
- Homework Statement
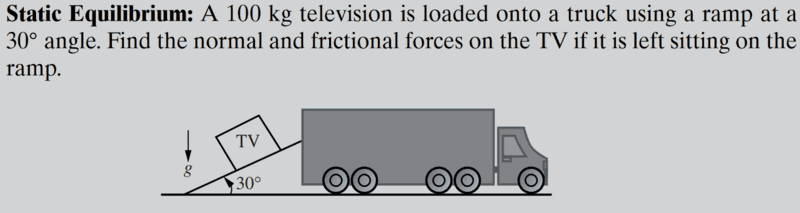
- In picture
- Relevant Equations
- Cos(x), sin(x), angle addition/subtraction.
I'm not really asking for a solution for this problem I just want to clear up a confusion I have.
Why are they multiplying the weight by the sin and cosine of the 30-degree angle?
Isn't weight not affected by anything since it's constant?
Also is the angle of friction 0 because it's a straight line?
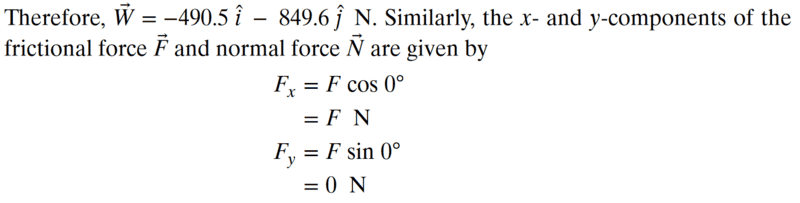
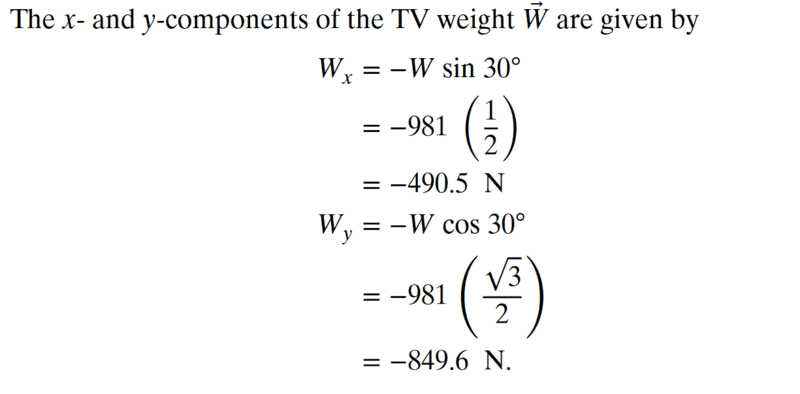
Why are they multiplying the weight by the sin and cosine of the 30-degree angle?
Isn't weight not affected by anything since it's constant?
Also is the angle of friction 0 because it's a straight line?