Increase Of Rotational Inertia While Motion Occurs

[Bashyboy]

The puzzle is:

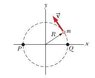
"The figure below represents a small, flat puck with mass m = 2.24 kg sliding on a frictionless, horizontal surface. It is held in a circular orbit about a fixed axis by a rod with negligible mass and length R = 1.03 m, pivoted at one end. Initially, the puck has a speed of v = 4.63 m/s. A 1.40-kg ball of putty is dropped vertically onto the the puck from a small distance above it and immediately sticks to the puck.

(a) What is the new period of rotation?

(b) Is the angular momentum of the puck–putty system about the axis of rotation constant in this process?

(c) Is the momentum of the system constant in the process of the putty sticking to the puck?

(d) Is the mechanical energy of the system constant in the process?"

-----------------------------------------------------------------------------------------

I was able to solve part (a).

For part (b), even though there is a collision, causing the putty and the puck to exert a force on each other, the forces are balanced, meaning the net force is zero, and the angular momentum is conserved. Is that right? So momentum would be conserved?

For part (c), didn't we sort of answer this question in part (b)?

For part (d), the answer is that mechanical energy is not conserved (constant) in the process. Why isn't it, though? Yes, I admit that the force of gravity pulls on the piece of putty, having it descend into the puck; there is force, but it is not being applied over a distance (work) to cause its state of energy to change--the force isn't even in the same direction as the motion, it is perpendicular to it.

 

[cosmic dust]

Even if forces were not zero during colision, they are perpendicular to the direction of motion, so they don't have to be considered. Angular momentum is preserved during the process and this is the key to the answer. Calculate angular momentum (L=Ιω) defore and after the colision, using the correct moments of inertia (there is a change in the mass of the rotating object but not a change in radius of rotation), Angular velocity before colision is known (ω=v/R) but unkown after the colision. Equate the two expressions of angular momentum and find angular velocity (it should be about 62% of the initial).
b) correct
c) almost. calculate momentum (mv) before and after colision. They should be the same.
d) When the putty stuck to the puck, it had not angular momentum, so it had to obtain some in order to move in circular orbit. That is why the angular velocity decreased: the putty "stole" angular momentum from the puck, as much as it needed to co-rotate with the puck. But putty also needed rotational energy, that is where the loss of energy came from. Although there is not an applied external force to the system, there is a inertial force that is opposed to the direction of motion. That inertal force is caused by the non-moving putty that is accelerated to reach the initial velocity.

 

[Bashyboy]

For part (c), are you saying that the momentum is conserved? Because the answer key says it isn't

 

[cosmic dust]

Then this is a trick question. Althought the magnitude of momentum is conserved (to see it, divide both sides of angular momentum conservation equation by R) it's direction is never constant (it's not before nor after the collision). Since momentum is defined as a vector, then it is not constant. The answer would be positive if it was referring about it's magnitude only

 

[Nickie]

I would like to clarify and expand on some of the concepts mentioned in the puzzle. First, let's define rotational inertia. Rotational inertia, also known as moment of inertia, is a measure of an object's resistance to changes in its rotational motion. It is dependent on the object's mass and its distribution from the axis of rotation. In this puzzle, the rotational inertia of the puck increases when the putty is dropped onto it because the mass of the system increases and the distribution of that mass changes.

Now, let's address the questions presented in the puzzle. For part (a), the new period of rotation can be calculated using the equation T = 2π√(I/mR^2), where T is the period, I is the rotational inertia, m is the mass, and R is the radius of rotation. Using the given values, we can calculate the new period of rotation to be approximately 3.07 seconds.

For part (b), you are correct in stating that the angular momentum of the system is conserved. This is because the forces between the puck and the putty are internal forces and do not change the total angular momentum of the system.

For part (c), the momentum of the system is also conserved. This can be seen by applying the law of conservation of momentum, which states that in a closed system, the total momentum remains constant. In this case, the system is closed as no external forces are acting on it.

For part (d), it is true that the mechanical energy of the system is not conserved in this process. This is because the collision between the putty and the puck is not perfectly elastic, meaning some energy is lost in the form of heat and sound during the collision. Additionally, the force of gravity does work on the putty as it falls onto the puck, causing a change in its gravitational potential energy.

In conclusion, the increase in rotational inertia while motion occurs is due to the addition of mass to the system and the redistribution of that mass. The angular momentum and momentum of the system are both conserved, while the mechanical energy of the system is not constant due to the non-elastic collision and work done by gravity.