Induced current in conductor moving circularly in constant B-field

[Waxbear]

Homework Statement

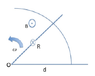
A light bulb with resistance R is attached on a metal rod which is rotating around the point O on the figure. The metal rod is in contact with an electrical conductor which is a part of a circle with radius d. The metal rod and the circular electrical conductor is a closed circuit. The rod now rotates with angular velocity \omega through the constant magnetic field pointing out from the paper.

a)

Find an expression for the induced current through the light bulb, expressed in terms of \omega, d, B and R.

Homework Equations

IR=vBr

where v is the tangential speed of the rod perpendicular to the B-field (every speed is perpendicular to the B-field, since we are looking at a plane) and r is the length of the rod moving at this speed.

I=\frac{\omega Br^{2}}{R}

v substituted for \omega r

The Attempt at a Solution

Since the every part of the rod is moving with different linear speeds, we should integrate the RHS from the 0 to d with respect to r and that should be it right?

i get:

I=\int^{d}_{0}\frac{\omega Br^{2}}{R}

I=\frac{d^{3}B\omega}{3R}

But when i look up the solution it says:

I=\frac{Bd^{2}\omega}{2R}

so who's right?

Edit: Problem solved!

 

[Waxbear]

Maybe i should add that RI=vBr is derived from Faradays law of induction, stating that the induced EMF is equal to the closed path integral of E+v X B with respect to l (path of the circuit), and Ohm's law stating that the EMF is equal to RI when looking at the entire circuit. I only integrate over the rod since this is the only thing moving relative to the B-field. The cross product in faradays law reduces to the magnitudes of v and B multiplied, since they are always perpendicular to each other in this problem and since i only need to find the magnitude of the EMF.

 

[Waxbear]

Nevermind i solved it!

After reading my last post over, i realized that i should use Faradays law of induction as the more general law, rather than IR=vBl which is a solution to Faradays law in a particular situation. I then obtained the same answer as in the solutions sheet.