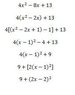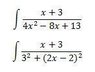mike01
- 9
- 0
Integral Help??Newbie
I apoligize in advance I am a newibe to this forum..
integral [(x+3)/(4x^2-8x+13)]
I am currently studying CalcII we Just got into evaluating integrals by completing the square in the denometer however I cannot get this one to work out. I attempted to evaluate by completing the square I got 9+(2x-2)^2 but I do cannot get a substitution to the X+3dx, I tried to split it into two with the X/ and the 3/ but again get stumped at the 3/. Just looking for a little guidance that’s all. Thanks in advance for everyone’s help.
I apoligize in advance I am a newibe to this forum..
Homework Statement
integral [(x+3)/(4x^2-8x+13)]
Homework Equations
The Attempt at a Solution
I am currently studying CalcII we Just got into evaluating integrals by completing the square in the denometer however I cannot get this one to work out. I attempted to evaluate by completing the square I got 9+(2x-2)^2 but I do cannot get a substitution to the X+3dx, I tried to split it into two with the X/ and the 3/ but again get stumped at the 3/. Just looking for a little guidance that’s all. Thanks in advance for everyone’s help.
Last edited: