Interference in electron conductance through e.g. molecule?

[jarekduda]

Imagine attaching electrodes to a complex sample, e.g. a semi-conductor or a single chemical molecule, leading to some electric current.
Can we decompose this electron flow into local flows? - like locally attaching amperometer and counting what fraction of electrons flow directly between given two atoms, or some larger parts of the system, like while analyzing electric circuits. In other words, can we imagine electron current as diffusion driven by electric field? - like explained in basic education.

While the above seems natural and intuitive, it was basically given up a half a century ago due to problems with modelling semiconductors. The issue is that standard diffusion models lead to to nearly uniform stationary probability distribution. Hence, attaching electric field we would get electron flow - wrongly predicting that semiconductor is a conductor.

In contrast, quantum mechanics predicts strongly localized (Anderson) probability distribution, prisoning the electrons and preventing conductance. Here are examples of electron density graphs for surface of semiconductor from 2010 Science article (its slides) using tunneling microscope (STM) - having complex localized patterns:

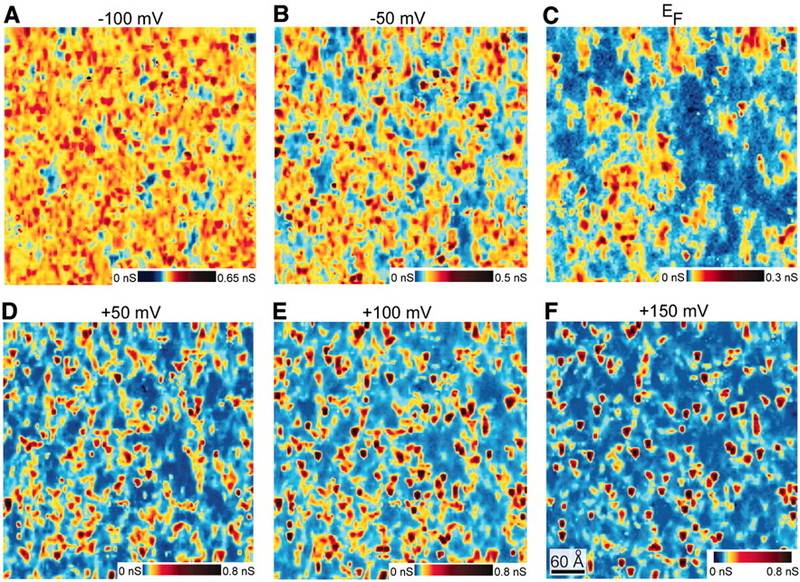
This disagreement enforced the quantum view: with interfering waves of electrons.

However, it turns out that standard diffusion models often only approximate the (Jaynes) principle of maximum entropy: "the probability distribution which best represents the current state of knowledge is the one with largest entropy", required by statistical physics models. This approximation is repaired in Maximal Entropy Random Walk (MERW), which turns out to have the missing localization property (PRL article) - leads to stationary probability distribution exactly as predicted by QM: of quantum ground state.

Here is example of evolution of standard random walk (GRW) and MERW on 40x40 lattice with cyclic boundary conditions, which is defected: all but marked vertices (squares) have additional self-loop (degree is 4 or 5):

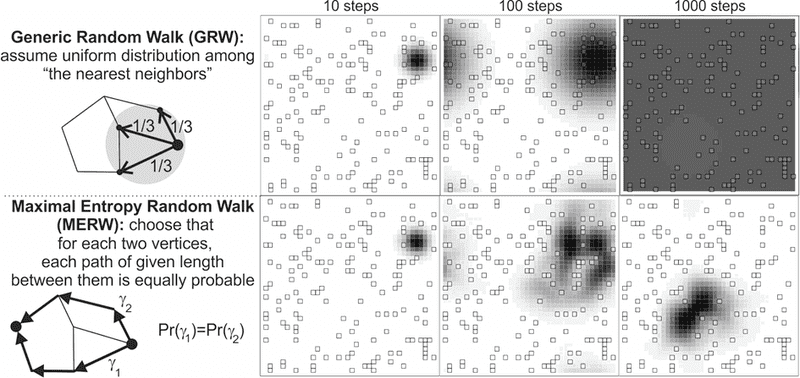
So MERW can be seen as some "quantum correction to diffusion models", e.g. here is a simple semiconductor simulator. However, it is not QM, it completely ignores interference-like phenomena. But while complete quantum conductance calculations are usually too expensive for our computers, MERW-based diffusion is relatively accessible, still having some crucial quantum properties - the question is importance of interference this approximation neglects.

So can we ask about local electron flows in complex conductance situations?
How important is interference in electron conductance? E.g. through aromatic ring of a molecule? Through graphene?

 

[jarekduda]

Understanding electron conductance in nanoscale is currently extremely important and difficult basic problem: transistors in our processors are reaching size of single atoms, there is considered electronics based on single molecules.
Complete quantum considerations are usually just too expensive, requiring even exponential growth of computational cost with system size.

However, in standard macroscopic electronics the situation is quite clear - using two Kirchhoff's laws we can write set of equation and get electric currents, e.g.

The found currents allow to answer questions: what percentage of electrons flow through a given wire,
or for a fork: what is probability of electron choosing a given path ... so mathematician would say that we have a stochastic model for electron behavior.

But what happens when reducing the scale?
E.g. imagine a semiconductor, and model it as a lattice of 1um x 1um x 1um cubes, which are small but no too small ("classical") - we should be able to ask about electron flows through different surfaces of such cubes - again be able to imagine it as an electric circuit, decompose into local electron flows, see as a stochastic model for electron behavior.

Now let's reduce these cubes - down to "cubes" being single atoms of e.g. a regular lattice - can we still decompose such conductance into local flows? Imagine attaching a nano-amperometr and asking what fraction of electrons flow directly between given two atoms?
Analogously for molecular electronics - can we imagine such molecule as an electric circuit? Ask what fraction of electrons flow through a given chemical bond?

In this scale we would like to use a random walk/diffusion model for electron - while the standard stochastic models usually give wrong answers, doing it right: accordingly to the maximal entropy principle, such MERW-based model is no longer in disagreement with basic quantum prediction, like stationary probability being exactly as for the quantum ground state.

In contrast to complete quantum calculations, MERW is relatively accessible (simple simulator) ...
So one question is how to choose the details - MERW uses Boltzmann distribution among trajectories, requiring to assign energy to transition between all pairs of neighboring atoms.
But more important issue is that MERW is not QM - it completely ignores interference - so the real question here is: how important interference is in electron conductance?