Widdekind
- 132
- 0
In the Schwarzschild Metric, the curvature of space around the gravitating mass can be described by the Flamm Paraboloid:
QUESTION: Does this mean, that rather than mass "bending the fabric of Spacetime 'downwards'" -- a la the "Rubber Sheet" analogy -- that mass actually bends the fabric of Spacetime about it "upwards" ?
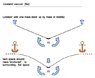
ANALOGY: Take a long blade of grass. It's straight representing a flat 1D "Lineland" space. Now, bend the blade of grass at some spot in the middle. That represents the curving of space caused by a massive body, "at the point of bend". But, the result is not so much that the "point of bend" bends downwards, but that both tips of the blade of grass bend upwards.
Can this be construed as an accurate interpretation of the Flamm Paraboloid ? Perhaps, if you "embed" a roughly Schwarzschild-esque solution, for a star (say), in a larger Cosmological fabric of Spacetime, then those "tips of the blade of grass" are "anchored" into that larger fabric, so that when the star tries to bend those tips upward, it actually "pushes itself downwards" ??
I have tried to illustrate my questions w/ the attached figure below:
w(r) = 2 \sqrt{r_{s} (r - r_{s})}
Unlike the Newtonian depiction of Gravitational Potential Wells (U = - G M / r) which decrease inwards, the Flamm Paraboloid increases outwards.QUESTION: Does this mean, that rather than mass "bending the fabric of Spacetime 'downwards'" -- a la the "Rubber Sheet" analogy -- that mass actually bends the fabric of Spacetime about it "upwards" ?
ANALOGY: Take a long blade of grass. It's straight representing a flat 1D "Lineland" space. Now, bend the blade of grass at some spot in the middle. That represents the curving of space caused by a massive body, "at the point of bend". But, the result is not so much that the "point of bend" bends downwards, but that both tips of the blade of grass bend upwards.
Can this be construed as an accurate interpretation of the Flamm Paraboloid ? Perhaps, if you "embed" a roughly Schwarzschild-esque solution, for a star (say), in a larger Cosmological fabric of Spacetime, then those "tips of the blade of grass" are "anchored" into that larger fabric, so that when the star tries to bend those tips upward, it actually "pushes itself downwards" ??
I have tried to illustrate my questions w/ the attached figure below: