doopa
- 6
- 1
- TL;DR
- I want to understand how one can go about estimating the mass of a central object given the a graph the orbital motion of S2, or any given star for that matter.
During one of my class lectures, we were shown a graph of star S2's orbit motion (shown at the bottom of this post) and was told to try and figure out how to find the mass of the central object using Kepler’s 3rd law in solar units, as shown below:
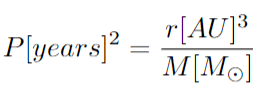
We were also given a hint to use the arcsec relation and read the radius of the orbit from the image, as shown below:
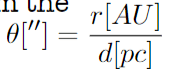
From my notes, it looks like we had to use the declination value of 0.1, but I still don't understand how exactly we got to that point. Does anyone happen to know why this is and how to generally use these types of graphs to estimate the mass of a central object?
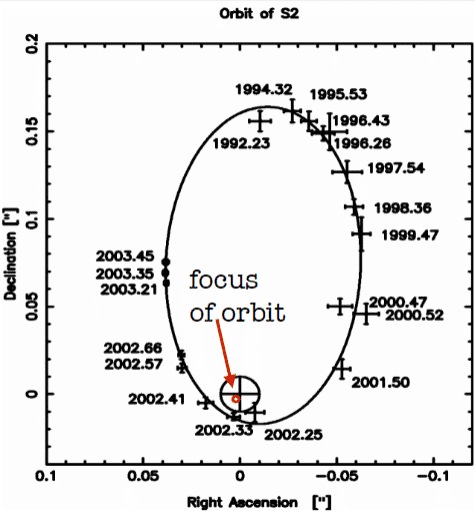
We were also given a hint to use the arcsec relation and read the radius of the orbit from the image, as shown below:
From my notes, it looks like we had to use the declination value of 0.1, but I still don't understand how exactly we got to that point. Does anyone happen to know why this is and how to generally use these types of graphs to estimate the mass of a central object?