ElectronicTeaCup
- 23
- 1
Summary:: Question: Show that the segment of a tangent to a hyperbola which lies between the asymptotes is bisected at the point of tangency.
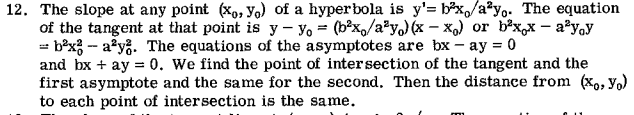

From what I understand of the solution, I should be getting two values of x for the intersection that should be equivalent but with different signs. However, I get
$$x=\frac{b^{2} x_{1}-a^{2} y_{1}^{2}}{a y_{1} b+b^{2} x_{1}}$$ and $$x=-\frac{b^{2} x_{1}-a^{2} y_{1}^{2}}{a b y_{1}-b^{2} x_{1}}$$
as the x-coordinates of the intersects with the two asymptotes. But these are not equivalent, am I making a mistake somewhere?
From what I understand of the solution, I should be getting two values of x for the intersection that should be equivalent but with different signs. However, I get
$$x=\frac{b^{2} x_{1}-a^{2} y_{1}^{2}}{a y_{1} b+b^{2} x_{1}}$$ and $$x=-\frac{b^{2} x_{1}-a^{2} y_{1}^{2}}{a b y_{1}-b^{2} x_{1}}$$
as the x-coordinates of the intersects with the two asymptotes. But these are not equivalent, am I making a mistake somewhere?