Intuition on Newton's Spinning Bucket

[Shreya]

Homework Statement

Why does the water move up the walls of the container and away from the axis of rotation?
How does the bucket communicate its motion to the water?

Relevant Equations

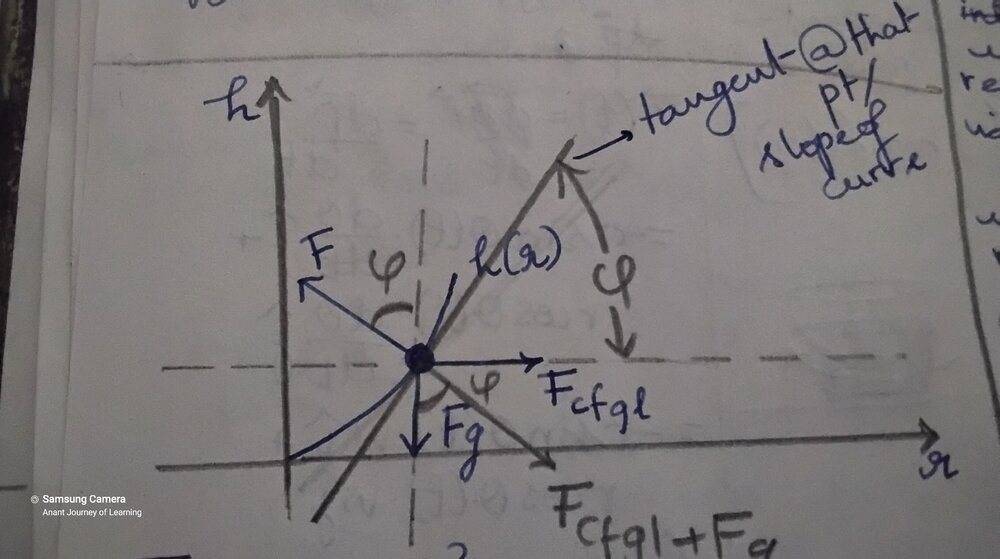
h(r) = ((wr)^2/2g) + h(0)

Pls Be Kind to answer.
I have understood the derivation of the parabolic shape by equating the normal force, gravity and the centrifugal force. But this derivation begins with the fact that water is at equilibrium.
I want an understanding (quantitative or qualitative) of why the water which was flat in the beginning climb up the walls of the container. What force causes it to?
How does the bucket transfer its motion to the water?
(And can this be understood with centripetal force and not centrifugal force?)
Thank you very much

 

[Halc]

The water assumes the shape due to the motion of the water, not the bucket. There is no force causing the motion outward. That's just the water's own inertia. The water 'wants' to continue in its direction of motion, but the bucket walls (moving or not) exert a centripetal force accelerating the water inward, preventing its motion in a straight line that would occur in the absence of the bucket walls.

Gravity also plays a role, pulling the water in a perpendicular direction to the centripetal force being applied by the bucket. Without gravity, the water would just move to the walls and spill out any end that wasn't closed.

 

[Shreya]

The water assumes the shape due to the motion of the water, not the bucket. There is no force causing the motion outward. That's just the water's own inertia. The water 'wants' to continue in its direction of motion, but the bucket walls (moving or not) exert a centripetal force accelerating the water inward, preventing its motion in a straight line that would occur in the absence of the bucket walls.

Gravity also plays a role, pulling the water in a perpendicular direction to the centripetal force being applied by the bucket. Without gravity, the water would just move to the walls and spill out any end that wasn't closed.

So does the water curl into a parabola due to its inertia?
Correct me i am wrong

 

[Halc]

Yes, a (quadratic) parabola, but my Latex isn't up to expressing the derivation.
Yes, the water is in equilibrium in that shape due to its inertia, inertia which it isn't going to lose if the system is frictionless. Of course a real bucket needs to spin along with the water to prevent its friction from slowing down the rotation of the water.

No water is accelerating outward, so there is no outward force. All the water (that isn't at the axis) is accelerating inward, so the bucket does exert an inward centripetal force.

 

[Lnewqban]

Using the bucket as frame of reference, creates the perception of a fictitious centrifugal force pushing the liquid radially out and up the walls of the container.

Please, see:
https://en.m.wikipedia.org/wiki/Fictitious_force

 

[Shreya]

Lnewqban, but the centrifugal force doesn't have an upward component so how does some water molecules rise up the mean position and some go lower?

 

[Halc]

Yes, relative to the rotating frame of the water/bucket, the water is stationary, and centrifugal force pushes the water to the sides into the parabola shape, and the bucket walls exert an equal an opposite centripetal force that exactly balances it, resulting in no net motion of anything.

Relative to any inertial frame, centrifugal force is fictitious.

Lnewqban, but the centrifugal force doesn't have an upward component so how does some water molecules rise up the mean position and some go lower?

The inertia (back to inertial frames again) moves the water up against the bucket walls, forcing it to go in the only direction it can, just like dumping the bucket on the ground makes the water spread out sideways despite the lack of any lateral force. That's fluid dynamics. Water does this. A bucket of bricks does not.

The water in the center goes down because there is less water at the center as it moves to the edges.

Viewed relative to the rotating frame, the centrifugal force moves the water up against the bucket walls, forcing it to go in the only direction it can. The water in the center goes down because there is less water at the center as it is pushed to the edges.

 

[Shreya]

I got it, Thank you very much!

 

[Lnewqban]

Lnewqban, but the centrifugal force doesn't have an upward component so how does some water molecules rise up the mean position and some go lower?

Yes, but each small volume of liquid must be in equilibrium of forces, otherwise it would move or flow in some direction.
Centripetal acceleration of any mass depends on the tangential velocity, which depends on its radius of rotation.

Just like you must lean your bicycle in a curve, that small volume closer to the walls of the container must "lean" more respect to the small volumes located closer to the center, which have a smaller tangential velocity.

Please, see:
https://www.me.psu.edu/cimbala/Learning/Fluid/Rigid_body/rigid_body.htm

Slowly but surely, the rotational energy of the bucket is transferred into the liquid.
Because the pressure inside the liquid depends on its vertical height, you could measure a higher pressure next to the walls than by the center of rotation.
That is the principle behind the centrifugal pumps.

 

[Shreya]

Lnewqban

Yes, but each small volume of liquid must be in equilibrium of forces, otherwise it would move or flow in some direction.
Centripetal acceleration of any mass depends on the tangential velocity, which depends on its radius of rotation.

Just like you must lean your bicycle in a curve, that small volume closer to the walls of the container must "lean" more respect to the small volumes located closer to the center, which have a smaller tangential velocity.

Please, see:
https://www.me.psu.edu/cimbala/Learning/Fluid/Rigid_body/rigid_body.htm

Slowly but surely, the rotational energy of the bucket is transferred into the liquid.
Because the pressure inside the liquid depends on its vertical height, you could measure a higher pressure next to the walls than by the center of rotation.
That is the principle behind the centrifugal pumps.

View attachment 281161View attachment 281162

Lnewqban, so the dV volume near the container must experience less centripetal force(more centrifugal force) than the dV near the axis of rotation
Similarly the dV in the outer edge must lean more so that the normal force can balance the centrifugal + Gravity.
Thus, we have a paraboloid.
More pressure near the walls is due to the weight of the volume of water above. I do not know the navier stokes equation, so I will check that article after I learn it (as soon as possible)
Am I right?
Please correct me if I am wrong.

 

[haruspex]

Lnewqban, but the centrifugal force doesn't have an upward component so how does some water molecules rise up the mean position and some go lower?

At any point on the surface, you have a vertical force tending to produce an acceleration g and a horizontal centrifugal force tending to produce an acceleration rω². These add to produce a tilted force. This must be normal to the local surface (or water would flow up or down the gradient).
This allows you to write a differential equation, and the solution is a parabola.

 

[Shreya]

At any point on the surface, you have a vertical force tending to produce an acceleration g and a horizontal centrifugal force tending to produce an acceleration rω². These add to produce a tilted force. This must be normal to the local surface (or water would flow up or down the gradient).
This allows you to write a differential equation, and the solution is a parabola.

By vertical force, do you mean the force due to the nearby water molecules. I have derived the parabola's equation.

But the derivation starts from a molecule which is already at equilibrium in the parabola. I consider this experiment to be happening on earth.
I wanted to know how (the process) does the water change its shape from flat to a parabola. By Halc's and Lnewqban's answer I have come to know that it is due the centrifugal force (due to inertia) that water changes shape to a parabola. Since water has nowhere else to go than up, it rises up under the influence of centrifugal force till the normal force can balance the centrifugal force.
Please correct me if I am wrong.

 

[haruspex]

By vertical force, do you mean the force due to the nearby water molecules.

No, I mean gravity. The nearby molecules produce the normal force.

I have derived the parabola's equation.

Good.

how (the process) does the water change its shape from flat to a parabola.

If you increase the rate of rotation then the centrifugal force increases and the net force (centrifugal +gravity) is no longer normal to the surface. It will have a component that points radially outward relative to the normal, pushing molecules up the slope.
This is no different than mentioned by other posts above. The point of my post #11 was how to derive the equation.

 

[haruspex]

As an aside, this is rather different from what you see when you stir a cup of tea to produce a vortex. In that case it approximates irrotational flow, and the tangential velocity is inversely proportional to the radius, except near the centre.

 

[Shreya]

As an aside, this is rather different from what you see when you stir a cup of tea to produce a vortex. In that case it approximates irrotational flow, and the tangential velocity is inversely proportional to the radius, except near the centre.

I was already confusing both and trying to find an analogy there. Thanks for that piece of information.

 

[Shreya]

If you increase the rate of rotation then the centrifugal force increases and the net force (centrifugal +gravity) is no longer normal to the surface. It will have a component that points radially outward relative to the normal, pushing molecules up the slope.

So that explains why as you increase the angular speed, the parabola gets deeper.

The inertia (back to inertial frames again) moves the water up against the bucket walls, forcing it to go in the only direction it can, just like dumping the bucket on the ground makes the water spread out sideways despite the lack of any lateral force. That's fluid dynamics. Water does this. A bucket of bricks does not.

The water in the center goes down because there is less water at the center as it moves to the edges.

Viewed relative to the rotating frame, the centrifugal force moves the water up against the bucket walls, forcing it to go in the only direction it can. The water in the center goes down because there is less water at the center as it is pushed to the edges.

Yes, but each small volume of liquid must be in equilibrium of forces, otherwise it would move or flow in some direction.
Centripetal acceleration of any mass depends on the tangential velocity, which depends on its radius of rotation.

Just like you must lean your bicycle in a curve, that small volume closer to the walls of the container must "lean" more respect to the small volumes located closer to the center, which have a smaller tangential velocity.

Thank you very much Halc, Lnewqban and Haruspex for your time and explanation.
Now I know why we get a parabola (by thinking wrt inertial and rotational frame) and know to derive it too...