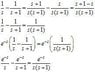Inverse Laplace transform with unit step function

[shaqywacky]

Hello again.

First off, I wasn't sure how to say this in the title but I'm not taking the inverse Laplace transform of a unit step function. I'm taking the Laplace transform of something that comes out to the unit step function.

I have this question, which is a similar version of the question I am trying to solve. This is also the solution but I have no idea what happened.

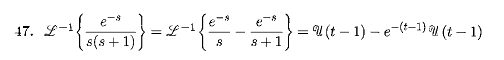
(sorry, I don't know why that is so small, click to make it bigger)

So the first part of that image is just the inverse Laplace transform I am trying to solve. The first step I saw was to do partial fractions. When I do that I get:
$\frac{e}{s+1} + \frac{1}{s}$
I'm omitting the inverse Laplace transform here because I don't know how to do it in latex.

But as you can see, the solution maunual got:
$\frac{e^{-s}}{s} - \frac{e^{-s}}{s+1}$

Clearly there is something I do not understand about this. I can get the correct answer after this, I just don't understand this step.

Any help would be greatly appreciated.

Thank you.

 

[JJacquelin]

Hi !
You question seems confused.
You must not use the same variable (s) for the function and for the Laplace transform of the function.
Please write clearly :
"The Laplace transform of f(x) is F(s)"
or
"The inverse Laplace transform of F(s) is f(x)"
Then, write clearly the expression of the known function : is it f(x) or F(s) ?

 

[shaqywacky]

I don't think I did. I never took any inverse Laplace transforms in my post. I'm talking about inside the Laplace transform. I didn't know how to use the Laplace transform in Latex, so I omitted it and made a note of it but I don't think I was being very clear. I'm just omitting the notation of the Laplace transform. So the equations I posted (besides the ones in the picture) are what's inside of the Laplace transform I'm trying to solve.

To try to clarify, I just don't understand the first step that is in the picture. So I don't see how they went from
$\frac{e^{-s}}{s(s-1)}$[/size]

to

$\frac{e^{-s}}{s} - \frac{e^{-s}}{s-1}$[/size]

Thanks.

 

[JJacquelin]

Hi !

Do you know how to write a polynomial fraction as a sum of simple terms ?
Have a look to the attachment :