Is Bubblesort Algorithm Correct?

[evinda]

Hello! (Wave)

Could you help me to prove the correctness of the following algorithm?

Bubblesort(A){
  int i, j;  
  for i from 1 to n {
      for j from n-1 downto i { 
           if (A[j] > A[j+1])
               swap(A[j], A[j+1]) 
           } 
  }
}

We could do this using induction, right? (Thinking)
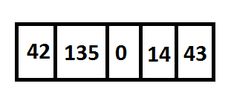
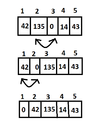
So, for [m] i=1 [/m] we compare [m] A[n-1] [/m] with [m] A[n] [/m] and if it holds that [m] A[n-1]>A[n] [/m] then we swap these two values.
So at the base case do we just say that the last two elements of the array are sorted?
What do we suppose at the induction hypothesis? (Thinking)

 

[Nono713]

Please observe how the bubble sort algorithm works on this video: https://www.youtube.com/watch?v=JP5KkzdUEYI (yours might be a variant that sorts from the smallest value, I haven't checked, but the two variants are equivalent up to reordering). Pay particular attention to the "limit" vertical line, and how everything on the right side of the line is automatically sorted. Note that at each iteration, the algorithm finds the largest element on the left of the line, and bubbles it up by repeated swaps. There's your induction hypothesis. Can you write down the inductive proof now that you have the intuition?​

 

[evinda]

So if we have for example this array:View attachment 3846

for [m]i=1 [/m] we will do the following:View attachment 3847

So this means that for [m] i=1 [/m] we compare pairwise the elements [m] A[n], A[n-1] [/m], [m] A[n-1],A[n-2] [/m], $\dots$, [m]A[2],A[1][/m] and if $A>A[i+1], i \in \{ 1, \dots, n-1 \}$ then we swap their values, right? (Thinking)