Is Convolution and Integration: A True Equality in Mathematics?

[Jhenrique]

I was verifying that:

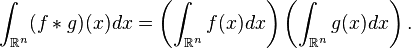
http://en.wikipedia.org/wiki/Convolution#Integration


But, I'd like to know if this equality is true:
\int f(x)g(x)dx \overset{?}{=} \int f(x)dx \ast \int g(x)dx

Subquestion: this theorem above can be applied in summation too?
\sum_{x}\left (f(x)\ast f(x) \right )\overset{?}{=}\left(\sum_{x} f(x)\right)\left (\sum_{x} g(x) \right )
\sum_{x}f(x)g(x) \overset{?}{=} \sum_{x}f(x) \ast \sum_{x}g(x)
Thanks!

 

[pwsnafu]

But, I'd like to know if this equality is true:
\int f(x)g(x)dx \overset{?}{=} \int f(x)dx \ast \int g(x)dx

The easy way to check is differentiate both sides. What do you know about the derivative of the convolution.

 

[R136a1]

But, I'd like to know if this equality is true:
\int f(x)g(x)dx \overset{?}{=} \int f(x)dx \ast \int g(x)dx

But $\int f(x) dx$ and $\int g(x)dx$ are just real numbers, no? What is the convolution of two numbers?

 

[Jhenrique]

The easy way to check is differentiate both sides. What do you know about the derivative of the convolution.

That:

 

[Jhenrique]

But $\int f(x) dx$ and $\int g(x)dx$ are just real numbers, no? What is the convolution of two numbers?

No! The result is a function!

The easy way to check is differentiate both sides. What do you know about the derivative of the convolution.

Results: f(x) g(x) = f(x) * ∫ g(x) dx

But, my ask remains! My as ask now is f(x) g(x) is equal to f(x) * ∫ g(x) dx ?