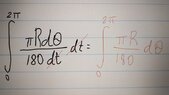Is It Possible? Solving Calculus Questions with Ease
- Context: Undergrad
- Thread starter NODARman
- Start date
-
- Tags
- Calculus
Click For Summary
SUMMARY
The discussion centers on the nuances of calculus, specifically the treatment of derivative notation such as ##\dfrac{d \theta }{dt}##. It is established that while this notation resembles a fraction, it is not mathematically valid to cancel the dt's. Instead, the chain rule illustrates how to manipulate these derivatives correctly, as shown in the equation ##\dfrac{d \theta }{dx} = \dfrac{d \theta }{dt} \cdot \dfrac{dt}{dx}##. Additionally, when integrating with respect to t, the bounds must be adjusted accordingly to ##\int_{t(0)}^{t(2\pi)}##.
PREREQUISITES- Understanding of calculus concepts, particularly derivatives and integrals.
- Familiarity with the chain rule in calculus.
- Knowledge of differential notation and its applications.
- Basic skills in manipulating mathematical expressions and equations.
- Study the implications of the chain rule in calculus.
- Learn about differential notation and its historical context in mathematics.
- Explore advanced integration techniques and their applications.
- Investigate the concept of limits and their role in calculus.
Students, educators, and professionals in mathematics or engineering fields who seek to deepen their understanding of calculus and its practical applications.
Similar threads
- · Replies 2 ·
- · Replies 9 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 5 ·
- · Replies 49 ·
- · Replies 4 ·
- · Replies 11 ·
High School
Vertical asymptote with an epsilon-delta proof?
- · Replies 4 ·
- · Replies 10 ·