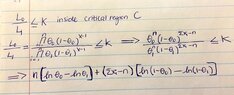SUMMARY
The discussion focuses on the application of the Neyman-Pearson Lemma in hypothesis testing, specifically for a single observation modeled by a geometric distribution. The critical region is defined by the likelihood ratio test, expressed as $$\frac{L(\theta_0 \ | \ x)}{L(\theta_1 \ | \ x)} \geq k$$. The calculation leads to the threshold $$k^{*} = 1 + \frac{\ln\left(\frac{k \theta_1}{\theta_0}\right)}{\ln\left(\frac{1-\theta_0}{1-\theta_1}\right)}$$, which determines the rejection region for the null hypothesis $H_0: \theta = \theta_0$. The type I error is also analyzed, confirming that the probability of incorrectly rejecting $H_0$ can be expressed as $$\mathbb{P}(X \geq k^{*} \ | \theta = \theta_0) = \alpha$$.
PREREQUISITES
- Understanding of the Neyman-Pearson Lemma
- Familiarity with likelihood ratio tests
- Knowledge of geometric distribution properties
- Basic concepts of hypothesis testing and type I error
NEXT STEPS
- Study the derivation of likelihood ratios in hypothesis testing
- Learn about type I and type II errors in statistical tests
- Explore generalizations of the Neyman-Pearson Lemma for multiple observations
- Investigate the implications of geometric distributions in real-world applications
USEFUL FOR
Statisticians, data scientists, and researchers involved in hypothesis testing and statistical inference, particularly those working with geometric distributions and likelihood ratio tests.