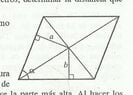
The area of a parallelogram is definitively calculated using the formula \( A = ab \sin \alpha \), where \( a \) and \( b \) are the lengths of the sides and \( \alpha \) is the angle between them. The discussion clarifies that \( a \) and \( b \) should not be interpreted as altitudes but rather as the lengths of the sides of the parallelogram. Any suggestion that the area could be represented as \( \frac{a}{b} \sin \alpha \) is incorrect, as this does not conform to the dimensional analysis of area, which requires a product of lengths.
PREREQUISITESStudents studying geometry, educators teaching mathematical concepts, and anyone interested in understanding the properties of parallelograms and trigonometric applications.
HallsofIvy said:
There must be something wrong here. The area of the parallelogram is $ab\sin\alpha$, where $\alpha$ is as in the diagram, but $a$ and $b$ have to be the sides of the parallelogram, not the perpendicular lengths shown in the diagram. In any case, the answer surely has to be $ab\sin\alpha$, not $a/b\sin\alpha$, which could never represent an area.leprofece said:
No, that cannot be right! An area is always a length times a length. A length divided by a length could never be an area. (Shake)leprofece said:
