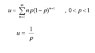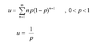Is the Proof of Geometric Progression in Probability Common Sense?
Click For Summary
Discussion Overview
The discussion revolves around the proof of a geometric progression in the context of probability, particularly focusing on the expected number of trials until the first success in a Bernoulli process. Participants express uncertainty about the proof's validity and its classification as "common sense" as stated in a statistics textbook.
Discussion Character
- Debate/contested
- Mathematical reasoning
- Technical explanation
Main Points Raised
- Some participants question the proof's validity, noting that key variables are not defined in the provided equations.
- Others suggest that the proof relates to the Binomial Theorem, indicating that the expected value can be derived from it.
- One participant proposes a method involving taking a derivative to solve the summation related to the geometric distribution.
- Several participants discuss the concept of memorylessness in geometric distributions, suggesting it is relevant to calculating expected values.
- There is disagreement about whether the problem is binomial or not, with some asserting it is a Bernoulli process rather than a binomial distribution.
- One participant claims to have proven the expected value associated with the geometric distribution, asserting that no textbook has provided this proof.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the classification of the distribution as binomial or Bernoulli, and there is ongoing debate regarding the validity of the proof and the definitions of the variables involved.
Contextual Notes
Some participants express concerns about convergence issues related to the summation, while others suggest that these concerns can be addressed through various mathematical approaches, including the use of Markov chains.
Similar threads
- · Replies 4 ·
- · Replies 1 ·
- · Replies 5 ·
- · Replies 13 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 5 ·
- · Replies 17 ·
- · Replies 4 ·