Is the Radial/Transverse coordinate system a non-inertial reference frame ?

[ezadam]

Hey guys,

I am having some problems with the concept of inertial/non-inertial frames of reference and their applications in engineering dynamics. So I've learned that a given frame of reference is defined to be non-inertial when something in the studied system can only be explained through fictitious forces such as the Centrifugal one.

Now, let's take as an example the motion of a block that can slide freely on a frictionless arm that rotates in a horizontal planewith a constant rate over a hinge. Here's a sketch of what I'm talking about:

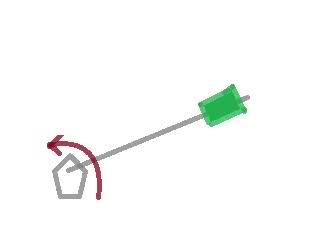
So if we look into the radial direction of the block's motion, we find that there is no force acting in such a direction and thus accordingly, the block should theoretically not move in the radial direction. Surprisingly, that is not what happens as the block slides away due to its inertia.

Now how come does that happen if there are no radial forces ? Does that mean (according to my initial definition) that I should have accounted for some centrifugal force and thus that my somewhat rough force analysis should be based on a non-inertial frame of reference, ergo that radial/transverse force analysis is not an inertial reference frame ? Or do I have some huge misconception about the issue ?

Thanks in advance

 

[tiny-tim]

hey ezadam!

So if we look into the radial direction of the block's motion, we find that there is no force acting in such a direction and thus accordingly, the block should theoretically not move in the radial direction. Surprisingly, that is not what happens as the block slides away due to its inertia.

Now how come does that happen if there are no radial forces ? Does that mean (according to my initial definition) that I should have accounted for some centrifugal force and thus that my somewhat rough force analysis should be based on a non-inertial frame of reference, ergo that radial/transverse force analysis is not an inertial reference frame ? Or do I have some huge misconception about the issue ?

you can use either an inertial frame or a rotating frame

in an inertial frame, there is no radial force, so the radial acceleration must be zero, so r'' must be positive …

since radial acceleration = r'' - ω²r ​

in a rotating frame, there is a centrifugal force ω²r, so r'' = ω²r

 

[ezadam]

Thanks for the reply tiny-tim :)

The fact that in an inertial frame, \ddot{r} is positive is what bothers me ... How can the block, physically speaking, move if there is no force responsible for its radial motion ? I understand your point mathematically but I still have some trouble understanding it intuitively :/

And also, what is the meaning of the block having a zero radial acceleration component while it is still moving radially ? Again, the mathematics of it make sense to me, but its physics is what confuses me the most ... What is the real meaning of radial acceleration ?

 

[tiny-tim]

And also, what is the meaning of the block having a zero radial acceleration component while it is still moving radially ? Again, the mathematics of it make sense to me, but its physics is what confuses me the most ... What is the real meaning of radial acceleration ?

sorry , you're going to have to convince yourself on this one …

try drawing velocity vectors

 

[ezadam]

Yeah I somehow pushed myself to understand it :) It's just that it's the first time that in a physics/mechanics course, I am exposed to a such an explicit expression of the effect of inertia on the kinematics of a certain body. Thanks for your help !