Is the trefoil knot truly unknottable or is there a way to simplify it?

[DaveC426913]

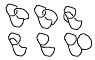
I was watching a video online about something completely different, but in the background I saw a computer monitor displaying an object similar to this.

Can this be topologically reduced to a simpler shape? Such as a simple one-, two- or three-hole doughnut? Or is it an irreducibly complex surface?

or three-hole

 

[Spinnor]

I think it only appears to be linked. You can change the object topologically to unlink it and you get three holes? I am having a hard time sketching the operations.

 

[Spinnor]

Hope this makes sense.

 

[WWGD]

You can try using some knot invariants like knot coloring number (tricoloring). https://en.wikipedia.org/wiki/Tricolorability

 

[jedishrfu]

Reminds me of this video on numberphile:

 

[DaveC426913]

View attachment 215041Hope this makes sense.

Oh! Ah!
Yes that makes sense!

Is it valid?

 

[Spinnor]

Similar? I think so.

From, https://www.ocf.berkeley.edu/~wwu/c...rd=riddles_hard;action=display;num=1044308041

From, https://www.google.com/search?safe=...22.0..0j35i39k1j0i8i30k1j0i24k1.0.VjuFcOlrySk

 

[WWGD]

Reminds me of this video on numberphile:

Who are you calling an a hole ? ;).

 

[DaveC426913]

Is it valid?

Yes, it is. I sketched it up a bit today, and you* are completely right! *Spinnor

I tried a few other shapes, even some apparent knots, and they can be reduced to simple shapes with holes.

Are there shapes that cannot be reduced below a certain level of complexity? Are there bona fide knots in topology?

 

[WWGD]

Yes, it is. I sketched it up a bit today, and you* are completely right! *Spinnor

I tried a few other shapes, even some apparent knots, and they can be reduced to simple shapes with holes.

Are there shapes that cannot be reduced below a certain level of complexity? Are there bona fide knots in topology?

Yes, there are " unnoktable" knots, e.g., the trefoil knot. Often you determine these are "genuine" knots by using invariants, i.e., properties intrinsic to knots, such as tricolorability https://en.wikipedia.org/wiki/Tricolorability. You can show the trefoil allows for tricolorability (i.e., painting the figure in 3 colors while satisfying certain conditions) while the unknot does not,which shows the two to be inequivalent ( or, more technically, " non-isotopic" ). Formally, a 3D knot is a copy of the circle that allows for twisting and bending of the circle , but do not allow for tearing , a.k.a $S^1$ under some functions called a homeomorphism. 2 images of the circle are considered equivalent if one can be deformed into another along special kinds of maps (" ambient isotopies"). Spinnor made use of this result by showing that the figure you presented can be deformed into the " unknot" by allowable moves; these moves are also called " Reidemeister" moves.

TL; DR: Equivalent knots share some properties, like the tricolorability property described above. Conversely, knots that do not share these properties are inequivalent as knots. Since trefoil and standard unknot do not share the tricolorability property, trefoil is a non-trivial knot.

 

[DaveC426913]

Yes, there are " unknottable" knots, e.g., the trefoil knot.

I guess that would explain its presence on the cover of my high school functions textbook, that I till remember from 35 years ago.

Almost makes me think they put it there to pique my curiosity...

 

[WWGD]

I guess that would explain its presence on the cover of my high school functions textbook, that I till remember from 35 years ago.

Almost makes me think they put it there to pique my curiosity...

View attachment 215120

Seems to have worked, albeit with some delay, I guess.

 

[jedishrfu]

I guess that would explain its presence on the cover of my high school functions textbook, that I till remember from 35 years ago.

Almost makes me think they put it there to pique my curiosity...

View attachment 215120

Your yearbook one is topologically different from the original drawing as there are no connection nodes.

 

[DaveC426913]

Your yearbook one is topologically different from the original drawing as there are no connection nodes.

??

In post 9 I asked about more complex knots. WWGD referred to the unknottable trefoil knot, in post 10 - subsequent to which I responded, in post 11.

So, yes. It's different.