Discussion Overview
The discussion revolves around the possibility of generating entangled photons with fixed polarization. Participants explore theoretical implications, practical challenges, and the relationship between entanglement and polarization states, with a focus on implications for computer simulations.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
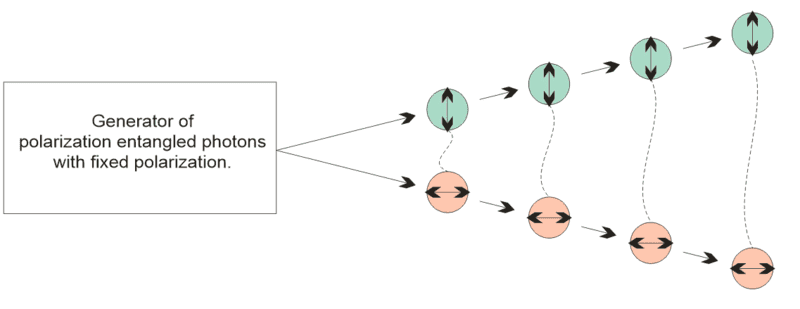
- One participant questions whether a generator of entangled photons with fixed polarization exists or if it is theoretically possible, citing a need for this knowledge for computer simulations.
- Another participant suggests that while state preparation can be theoretically flexible, practical implementation may be challenging.
- A participant references spontaneous parametric down-conversion and expresses initial belief in the possibility of such a generator, but later acknowledges that entangled photons typically do not have definite polarization.
- Discussion includes the no-communication theorem, which states that shared entanglement cannot be used to transmit information, and contrasts it with the no-teleportation theorem.
- Some participants assert that it is contradictory for particles to be both polarization entangled and have fixed polarization, emphasizing that entangled particles exist in superposition until measured.
- There is a debate regarding the interpretation of diagrams related to entangled photons, with some participants arguing that the majority of cases do not yield entangled photons.
- Mathematical reasoning is presented regarding the equivalence of superpositions in different polarization bases, with discussions on vector addition and transformations.
- Clarifications are made about the nature of entangled photons in specific polarization states, with some participants asserting that knowledge of polarization is limited to perpendicular states.
Areas of Agreement / Disagreement
Participants express differing views on the feasibility of generating entangled photons with fixed polarization. While some assert it is impossible due to the nature of entanglement, others propose that it may be achievable under certain conditions, leading to an unresolved debate.
Contextual Notes
Participants highlight limitations in understanding the implications of entanglement and polarization, as well as the dependence on specific definitions and interpretations of diagrams. There are also unresolved mathematical steps regarding superposition and transformations.