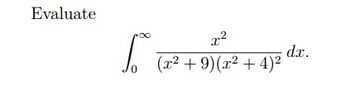Discussion Overview
The discussion revolves around the methods from real analysis that can be applied to solve complex integrals, particularly in the context of a worksheet problem from a real analysis class. Participants explore various approaches, including convergence considerations and specific techniques for integration.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants suggest that the problem likely requires a method from real analysis, questioning whether the goal is to test differentiating skills.
- There is a discussion about the necessity of proving the convergence of the integral, with some participants expressing uncertainty about this requirement.
- One participant proposes that the integrand's behavior can be analyzed to argue for convergence, noting that the denominator is strictly positive and bounded away from zero.
- Another participant mentions that evaluating the integral directly could provide insight into convergence, although this approach raises questions about the reliability of numerical results for divergent integrals.
- There is a mention of using the Cauchy Residue theorem after simplifying the integral, while another participant suggests a substitution method for finding an indefinite integral.
- Concerns are raised about the potential for misleading numerical results from improper integrals, with references to the need for careful consideration of convergence in both integrals and series.
Areas of Agreement / Disagreement
Participants express differing views on the necessity of proving convergence for the integral, and there is no consensus on whether evaluating the integral numerically is a reliable method in cases of divergence. The discussion remains unresolved regarding the best approach to take.
Contextual Notes
Participants highlight limitations in their arguments, such as the need to define convergence and the conditions under which integrals may yield misleading numerical results. There is also an acknowledgment of the complexity involved in discussing convergence in the context of improper integrals.