- #1
Math Amateur
Gold Member
MHB
- 3,990
- 48
I am reading Reinhold Remmert's book "Theory of Complex Functions" ...I am focused on Chapter 1: Complex-Differential Calculus ... and in particular on Section 2: Complex and Real Differentiability ... ... ...I need help in order to fully understand the relationship between complex and real differentiability ... ...Remmert's section on complex and real differentiability reads as follows:View attachment 8529
View attachment 8530
View attachment 8531In the above text from Remmert, we read the following ... ... just below 1. Characterization of complex-differentiable functions ... ...
" ... ... If \(\displaystyle f : D \to C\) is complex-differentiable at \(\displaystyle c\) then ...$\displaystyle \lim_{ h \to 0 } \frac{ f(c + h ) - f(c) - f\, ' (c) h }{ h} = 0$From this and (1) it follows immediately that complex-differentiable mappings are real differentiable and have \(\displaystyle \mathbb{C}\)-linear differentials ... ...
... ... ... "
Can someone please explain (formally and rigorously) how/why
(i) it follows from the limit immediately above and (1) that complex-differentiable mappings are real differentiable ... ...
(ii) it follows from the limit immediately above and (1) that complex-differentiable mappings have \(\displaystyle \mathbb{C}\)-linear differentials ... ... (***NOTE: I suspect the answer to (i) is that the form of the two limits is essentially the same ... although I'm concerned about the presence of norms in one and not the other ... and also that we can identify \(\displaystyle \mathbb{C}\) with \(\displaystyle \mathbb{R}^2\) as a vector space ... is that correct?)Help will be appreciated ...
Peter
=======================================================================================
MHB readers of the above post may benefit from access to Remmert's section defining R-linear and C-linear mappings ... so I am providing access to that text ... as follows:
View attachment 8532
View attachment 8533Hope that helps ...
Peter
View attachment 8530
View attachment 8531In the above text from Remmert, we read the following ... ... just below 1. Characterization of complex-differentiable functions ... ...
" ... ... If \(\displaystyle f : D \to C\) is complex-differentiable at \(\displaystyle c\) then ...$\displaystyle \lim_{ h \to 0 } \frac{ f(c + h ) - f(c) - f\, ' (c) h }{ h} = 0$From this and (1) it follows immediately that complex-differentiable mappings are real differentiable and have \(\displaystyle \mathbb{C}\)-linear differentials ... ...
... ... ... "
Can someone please explain (formally and rigorously) how/why
(i) it follows from the limit immediately above and (1) that complex-differentiable mappings are real differentiable ... ...
(ii) it follows from the limit immediately above and (1) that complex-differentiable mappings have \(\displaystyle \mathbb{C}\)-linear differentials ... ... (***NOTE: I suspect the answer to (i) is that the form of the two limits is essentially the same ... although I'm concerned about the presence of norms in one and not the other ... and also that we can identify \(\displaystyle \mathbb{C}\) with \(\displaystyle \mathbb{R}^2\) as a vector space ... is that correct?)Help will be appreciated ...
Peter
=======================================================================================
MHB readers of the above post may benefit from access to Remmert's section defining R-linear and C-linear mappings ... so I am providing access to that text ... as follows:
View attachment 8532
View attachment 8533Hope that helps ...
Peter
Attachments
-
 Remmert - 1 - Complex and Real Differentiability - Section 2, Ch. 1 - PART 1 ... .png12.8 KB · Views: 55
Remmert - 1 - Complex and Real Differentiability - Section 2, Ch. 1 - PART 1 ... .png12.8 KB · Views: 55 -
 Remmert - 2 - Complex and Real Differentiability - Section 2, Ch. 1 - PART 2 ... .png48.6 KB · Views: 53
Remmert - 2 - Complex and Real Differentiability - Section 2, Ch. 1 - PART 2 ... .png48.6 KB · Views: 53 -
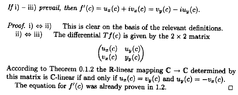 Remmert - 3 - Complex and Real Differentiability - Section 2, Ch. 1 - PART 3 ... .png11.6 KB · Views: 53
Remmert - 3 - Complex and Real Differentiability - Section 2, Ch. 1 - PART 3 ... .png11.6 KB · Views: 53 -
 Remmert - 1 - R-linear and C-linear Mappings, Ch. 0, Section 1.2 ... PART 1 .png16.1 KB · Views: 50
Remmert - 1 - R-linear and C-linear Mappings, Ch. 0, Section 1.2 ... PART 1 .png16.1 KB · Views: 50 -
 Remmert - 2 - R-linear and C-linear Mappings, Ch. 0, Section 1.2 ... PART 2 .png44.6 KB · Views: 49
Remmert - 2 - R-linear and C-linear Mappings, Ch. 0, Section 1.2 ... PART 2 .png44.6 KB · Views: 49