Is there an uncertainty in energy measurement in quantum mechanics?

[CGandC]

Let's say I have a system whose time evolution looks something like this:

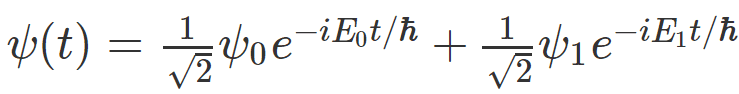
This equation tells me that if I measure energy on it, I will get either energy reading $E_0$ or energy reading $E_1$ , when I do that, the system will "collapse" into one of the energy eigenstates, $\psi_0$ or $\psi_1$ .

For example, if I have measured energy and have gotten $E_1$ , then , my system would be described by the wavefunction

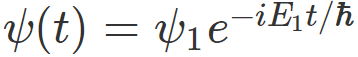
Now the question is:
If I refer to the last example , then, since I made energy measurement and have gotten $E_1$ in the measurement , then, how come is this even possible? isn't there uncertainty in every measurement? ( so that by measuring the energy , there's supposed to be some uncertainty in the measurement value of $E_1$ , but the value that was measured is exactly $E_1$ so this makes no sense to me because there is an infinite precision in the measurement )

In addition ,since now the wave function is collapsed to eigenstate corresponding to $E_1$ , then, each time I make energy measurement I will get only $E_1$ , this makes no sense to me, because isn't there uncertainty in the measurement? ( What I'm thinking is: when I make a measurement on the collapsed wave function , I will actually measure some other energy value which is close to $E_1$ but not exactly $E_1$ [ because of the uncertainty principle , and because each measurement of a physical paramter is actually an average value of that specific measurement ] )

 

[kuruman]

You are confusing quantum uncertainty with experimental uncertainty. The quantum uncertainty that is addressed in the uncertainty principle is an inherent feature of the wave description of matter; it has nothing to do with how accurate an instrument one has to measure a particle's momentum or energy.

 

[PeroK]

The uncertainty principle in general allows a variance of zero on some measureables. in the case of discrete energy values, theoretically the variance is zero for an eigenstate. But this does not violate any uncertainty principle.

 

[PeterDonis]

@CGandC please do not post equations as images; if you do that they cannot be quoted in replies, making it difficult to have a discussion. Please use the PF LaTeX feature to post equations directly in the thread. You can find info on that here:

https://www.physicsforums.com/help/latexhelp/

 

[CGandC]

The uncertainty principle in general allows a variance of zero on some measureables. in the case of discrete energy values, theoretically the variance is zero for an eigenstate. But this does not violate any uncertainty principle.

What are examples of more such measureables [ for whom the variance is zero and the measurement is theoretically exact , besides time ]?

 

[PeroK]

What are examples of more such measureables [ for whom the variance is zero and the measurement is theoretically exact , besides time ]?

Any physically realisable eigenstate has zero variance for the measurable in question. For example, energy, angular momentum, spin. In this sense, position and momentum are the exceptions, rather than the rule.

You're still confusing what the UP says with what you actually measure. The UP doesn't say and can't say that any measurement is "theoretically" exact. It doesn't put any constraints on how precisely you are able to measure something. That's the limitation of your experimental set-up. What the UP says is there there is an inherent variance in the measurements. To take an example:

If you roll a die, you definitely get a single number from 1-6. The expected value is 3.5 and the variance is about 2.9. These are inherent to the distribution, not to the measurement process. It's the same with energy eigenstates. If a state is an equal combination of two energy states, you get one or the other with equal probability when you measure it. How precise your measurement is depends on your setup.

In fact, you could say that the UP is not about measurement but about state preparation. And, instead of saying that you cannot measure position and momentum at the same time, you should say that the product of the variance of position and momentum measurements for a given state cannot be zero:

$\sigma_x \sigma_p \ge \frac{\hbar}{2}$

Note: $\sigma$ is standard deviation and variance is $\sigma^2$

 

[A. Neumaier]

This equation tells me that if I measure energy on it, I will get either energy reading $E_0$ or energy reading $E_1$.

Indeed, Born's rule claims that you get exactly this (independent of the uncertainty principle, which addresses different questions).

But as you correctly observed, Born's rule is nonsensical in this case. This is discussed at length in the thread '''Many measurements are not covered by Born's rule'', in particular, post #32, post #41, post #64 and later.

If a state is an equal combination of two energy states, you get one or the other with equal probability when you measure it. How precise your measurement is depends on your setup.

But one cannot get the two (usually irrational) values exactly, while you claim (in accordance with Born's rule) that one does.

 

[PeroK]

But one cannot get the two (usually irrational) values exactly, while you claim (in accordance with Born's rule) that one does.

A rational number in one system of units might be irrational in another. In any case, the issue of using a continuum in the theory of physics, where any measurement can only return one of a finite set of possibilities (determined by the measurement set up *) applies across all physics.

(*) E.g. an atomic clock is counting cycles and only has a finite number of possible readings. Yet, time is theoretically modeled as a continuum.

 

[A. Neumaier]

A rational number in one system of units might be irrational in another.

Sure. But the (in a real case more than two) energy levels of an atom (except for exactly solvable cases) are typically incommensurable among each other, so that no matter how you place the origin and how you choose the system of units, most of the energy levels will remain irrational.

the issue of using a continuum in the theory of physics, where any measurement can only return one of a finite set of possibilities (determined by the measurement set up) applies across all physics.

Yes, but it still implies that Born's rule for the measurement of discrete energy levels can be approximate only, whereas the standard claim is that Born's rule applies exactly.

 

[PeroK]

Yes, but it still implies that Born's rule for the measurement of discrete energy levels can be approximate only, whereas the standard claim is that Born's rule applies exactly.

It depends what you mean by exact. For example, theoretically, if you measure electron z-spin, then you have a equally likely combination of x-spins. But, in practice, you can never have two measurements set up exactly rotated by 90°. I don't see that that goes against the theory?

 

[A. Neumaier]

It depends what you mean by exact. For example, theoretically, if you measure electron z-spin, then you have a equally likely combination of x-spins. But, in practice, you can never have two measurements set up exactly rotated by 90°. I don't see that that goes against the theory?

This does not go against the theory, because you changed the subject. But this thread is about measuring energy levels, not spins.

 

[PeroK]

This does not go against the theory, because you changed the subject. But this thread is about measuring energy levels, not spins.

Can you explain the problem in terms of energy levels?

 

[A. Neumaier]

Can you explain the problem in terms of energy levels?

Consider a system with (for the sake of simplicity) finitely many energy levels $E_1,\ldots,E_N$. (The OP asked about the case$N=2$ and shifts the indices by 1, but his question applies more generally.) As stated, e.g., in Wikipedia, Born's rule claims that upon measuring the total energy $H$ of the system you get exactly one of the values $E_1,\ldots,E_N$. Note that exactness is essential to conclude from Born's rule the important formula $\langle A\rangle=tr \rho A$ figuring in much of formal (i.e. uninterpreted) quantum mechanics.

Assuming (as you seem to do) some choice of origin and units, measurements are rational numbers, the measurement results form an affine space of dimension 1 over the field of rationals. Thus getting all $E_i$ is impossible when the numbers $E_1,\ldots,E_N$ span over the rationals an affine space of dimension $d>1$. But the generic case is $d=N-1$. Thus there is no reason at all why, for any real quantum system with discrete energy spectrum and $N>2$ levels, one should get a dimension $d=1$! Even when one does, applying an external field would perturb the spectrum in a generally irrational way, increasing the dimension to $d=N-1$.

Therefore the exact validity of Born's rule for the measurement of discrete spectra is inconsistent with any practicable scheme for real measurements.

 

[PeroK]

Consider a system with (for the sake of simplicity) finitely many energy levels $E_1,\ldots,E_N$. (The OP asked about the case$N=2$ and shifts the indices by 1, but his question applies more generally.) As stated, e.g., in Wikipedia, Born's rule claims that upon measuring the total energy $H$ of the system you get exactly one of the values $E_1,\ldots,E_N$. Note that exactness is essential to conclude from Born's rule the important formula $\langle A\rangle=tr \rho A$ figuring in much of formal (i.e. uninterpreted) quantum mechanics.

Assuming (as you seem to do) some choice of origin and units, measurements are rational numbers, the measurement results form an affine space of dimension 1 over the field of rationals. Thus getting all $E_i$ is impossible when the numbers $E_1,\ldots,E_N$ span over the rationals an affine space of dimension $d>1$. But the generic case is $d=N-1$. Thus there is no reason at all why, for any real quantum system with discrete energy spectrum and $N>2$ levels, one should get a dimension $d=1$! Even when one does, applying an external field would perturb the spectrum in a generally irrational way, increasing the dimension to $d=N-1$.

Therefore the exact validity of Born's rule for the measurement of discrete spectra is inconsistent with any practicable scheme for real measurements.

I must confess I don't understand that argument or the conclusion. How would you test your theory?

 

[A. Neumaier]

I must confess I don't understand that argument or the conclusion. How would you test your theory?

For the total energy, Born's rule claims to lead to exact measurement of irrational (and in practice unknown) numbers, while it is clear that we cannot read such numbers from experiment. For example, it would mean that we would know from measurement the exact value of the Lamb shift. But we don't.

 

[CGandC]

I understood so far, but then, I encountered the following energy-time uncertainty relationship: $\Delta E \Delta t \geq \frac{\hbar}{2}$
But if energy and time could theoretically be measured exactly, then , this relationship is not fulfilled , but I assume I'm wrong about this, so , what does this uncertainty relationship mean? what does it refer to exactly? when does it apply?

 

[PeroK]

I understood so far, but then, I encountered the following energy-time uncertainty relationship: $\Delta E \Delta t \geq \frac{\hbar}{2}$
But if energy and time could theoretically be measured exactly, then , this relationship is not fulfilled , but I assume I'm wrong about this, so , what does this uncertainty relationship mean? what does it refer to exactly? when does it apply?

The energy-time uncertainty relationship is a much looser notion. You could look around the Internet. As a start, here's what Griffiths says in his book:

... persuade you that it is an altogether different beast. whose superficial resemblance to the position-momentum uncertainty principle is actually quite misleading.

Note, in particular, that in non-relativistic QM time is a parameter and not an observable. There is no operator that represents a measurement of time.

 

[A. Neumaier]

I understood so far, but then, I encountered the following energy-time uncertainty relationship: $\Delta E \Delta t \geq \frac{\hbar}{2}$
But if energy and time could theoretically be measured exactly, then , this relationship is not fulfilled , but I assume I'm wrong about this, so , what does this uncertainty relationship mean? what does it refer to exactly? when does it apply?

See the answers given in What is Δt in the time-energy uncertainty principle?