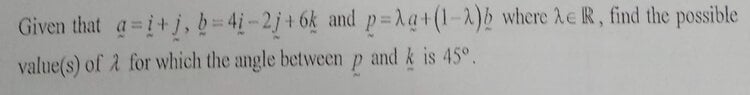SUMMARY
The discussion centers on the definition of the vector $\underline{k}$ in vector notation, specifically questioning whether $\underline{k} = \langle 0,0,1 \rangle$ is an established fact. Participants confirm that in standard Cartesian coordinates, $\underline{k}$ is indeed defined as the unit vector in the positive z-direction, represented as $\langle 0,0,1 \rangle$. This notation is universally accepted in vector mathematics and is critical for understanding three-dimensional space representation.
PREREQUISITES
- Understanding of vector notation and Cartesian coordinates
- Familiarity with unit vectors in three-dimensional space
- Basic knowledge of linear algebra concepts
- Ability to interpret mathematical notation
NEXT STEPS
- Study the properties of unit vectors in three-dimensional space
- Learn about vector operations such as addition and scalar multiplication
- Explore the application of vectors in physics, particularly in mechanics
- Investigate the role of vectors in computer graphics and 3D modeling
USEFUL FOR
Students of mathematics, physics enthusiasts, and anyone seeking to deepen their understanding of vector notation and its applications in various fields.