- #1
Pushoam
- 962
- 51
Equation 9.2.25 defines the inner product of two vectors in terms of their components in the same basis.
In equation 9.2.32, the basis of ## |V \rangle## is not given.
## |1 \rangle ## and ## |2 \rangle ## themselves form basis vectors. Then how can one calculate ## \langle 1| V \rangle ## ?
Do we have to assume that all of these vectors are given in the orthogonal basis with vectors given by
## \begin{bmatrix}
1
\\ 0
\end{bmatrix} ## and ## \begin{bmatrix}
0
\\ 1
\end{bmatrix} ## ?
Attachments
-
 upload_2018-8-19_18-29-6.png12.5 KB · Views: 1,471
upload_2018-8-19_18-29-6.png12.5 KB · Views: 1,471 -
 upload_2018-8-19_18-29-42.png22 KB · Views: 534
upload_2018-8-19_18-29-42.png22 KB · Views: 534 -
 upload_2018-8-19_18-31-30.png26.6 KB · Views: 568
upload_2018-8-19_18-31-30.png26.6 KB · Views: 568 -
 upload_2018-8-19_18-32-10.png21.1 KB · Views: 532
upload_2018-8-19_18-32-10.png21.1 KB · Views: 532 -
 upload_2018-8-19_18-35-13.png23.9 KB · Views: 579
upload_2018-8-19_18-35-13.png23.9 KB · Views: 579 -
 upload_2018-8-19_19-51-2.png14.8 KB · Views: 1,444
upload_2018-8-19_19-51-2.png14.8 KB · Views: 1,444 -
 upload_2018-8-19_19-55-44.png25.7 KB · Views: 4,583
upload_2018-8-19_19-55-44.png25.7 KB · Views: 4,583 -
 upload_2018-8-19_19-56-16.png17.6 KB · Views: 1,158
upload_2018-8-19_19-56-16.png17.6 KB · Views: 1,158 -
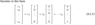 upload_2018-8-19_19-57-23.png6.1 KB · Views: 1,195
upload_2018-8-19_19-57-23.png6.1 KB · Views: 1,195 -
 upload_2018-8-19_19-57-59.png33 KB · Views: 1,351
upload_2018-8-19_19-57-59.png33 KB · Views: 1,351
Last edited: