MarkFL
Gold Member
MHB
- 13,284
- 12
Here is the question:
I have posted a link there to this topic so the OP can see my work.
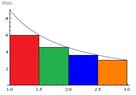
Area of the definite integral?
Find an approximation of the area of the region R under the graph of the function f on the interval [1, 3]. Use n = 4 subintervals. Choose the representative points to be the right endpoints of the subintervals.
f(x) = 9/x
I have posted a link there to this topic so the OP can see my work.