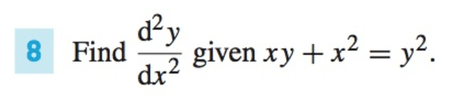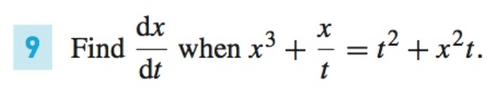Prove It
Gold Member
MHB
- 1,434
- 20
View attachment 5525
Since we have this relationship between x and y, as the two sides are equal, so are their derivatives. We just have to remember that as y is a function of x, any function of y is also a function of x, with the inner function "y" composed inside whatever is being told to do to the y. So to differentiate these parts the Chain Rule would be needed. All other rules like the product and quotient rules will still apply as well. Anyway, differentiating both sides with respect to x gives
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x}\,\left( x\,y + x^2 \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^2 \right) \\ x\,\frac{\mathrm{d}y}{\mathrm{d}x} + 1\,y + 2\,x &= \frac{\mathrm{d}y}{\mathrm{d}x}\,\frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^2 \right) \\ x\,\frac{\mathrm{d}y}{\mathrm{d}x} + y + 2\,x &= \frac{\mathrm{d}y}{\mathrm{d}x}\,\left( 2\,y \right) \\ y + 2\,x &= 2\,y\,\frac{\mathrm{d}y}{\mathrm{d}x} - x\,\frac{\mathrm{d}y}{\mathrm{d}x} \\ y + 2\,x &= \left( 2\,y - x \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \frac{y + 2\,x}{2\,y - x} \end{align*}$
This will be important for later. Going back a step and differentiating both sides with respect to x again we have
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x} \,\left( y + 2\,x \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left[ \left( 2\,y - x \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} \right] \\ \frac{\mathrm{d}y}{\mathrm{d}x} + 2 &= \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} + \left( 2\,\frac{\mathrm{d}y}{\mathrm{d}x} - 1 \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} \\ \frac{\mathrm{d}y}{\mathrm{d}x} + 2 &= \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} + 2\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 - \frac{\mathrm{d}y}{\mathrm{d}x} \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2 + 2\,\frac{\mathrm{d}y}{\mathrm{d}x} - 2\,\left( \frac{\mathrm{d}y}{\mathrm{d}x}\right) ^2 \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ 1 + \frac{\mathrm{d}y}{\mathrm{d}x} - \left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 \right] \end{align*}$
and since we already found that $\displaystyle \begin{align*} \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{y + 2\,x}{2\,y - x } \end{align*}$ that means
$\displaystyle \begin{align*} \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2 \, \left[ 1 + \frac{y + 2\,x}{2\,y - x} - \left( \frac{y + 2\,x}{2\,y - x } \right) ^2 \right] \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ \frac{\left( 2\,y - x \right) ^2 + \left( 2\,y - x \right) \left( y + 2\,x \right) - \left( y + 2\,x \right) ^2}{\left( 2\,y - x \right) ^2 } \right] \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ \frac{4\,y^2 - 4\,x\,y + x^2 + 2\,y^2 + 4\,x\,y - x\,y - 2\,x^2 - y^2 - 4\,x\,y - 4\,x^2}{\left( 2\,y - x \right) ^2} \right] \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ \frac{5\,y^2 - 5\,x\,y - 5\,x^2 }{\left( 2\,y - x \right) ^2} \right] \\ \frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= \frac{10\,\left( y^2 - x\,y - x^2 \right) }{\left( 2\,y - x \right) ^3} \end{align*}$View attachment 5526
Here x is a function of t, so again, to differentiate any x terms, we must use the Chain Rule.
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} \,\left( x^3 + x\,t^{-1} \right) &= \frac{\mathrm{d}}{\mathrm{d}t} \,\left[ t^2 \left( 1 + x^2 \right) \right] \\ \frac{\mathrm{d}x}{\mathrm{d}t} \, \frac{\mathrm{d}}{\mathrm{d}x} \, \left( x^3 \right) + \frac{\mathrm{d}x}{\mathrm{d}t} \, t^{-1} - x \, t^{-2} &= 2 \, t \, \left( 1 + x^2 \right) + t^2 \, \frac{ \mathrm{d}x }{ \mathrm{d}t } \, \frac{ \mathrm{d} }{\mathrm{d}x} \, \left( 1 + x^2 \right) \\ \frac{\mathrm{d}x}{\mathrm{d}t}\,\left( 3\,x^2 \right) + \frac{\mathrm{d}x}{\mathrm{d}t}\,t^{-1} - x \,t^{-2} &= 2\,t\,\left( 1 + x^2 \right) + t^2\,\frac{\mathrm{d}x}{\mathrm{d}t} \,\left( 2\,x \right) \\ 3\,x^2\,\frac{\mathrm{d}x}{\mathrm{d}t} + t^{-1}\,\frac{\mathrm{d}x}{\mathrm{d}t} - 2\,x\,t^2 \,\frac{\mathrm{d}x}{\mathrm{d}t} &= 2\,t + 2\,x^2\,t + x\,t^{-2} \\ t^2\,\left( 3\,x^2 + t^{-1} - 2\,x\,t^2 \right) \,\frac{\mathrm{d}x}{\mathrm{d}t} &= t^2\,\left( 2\,t + 2\,x^2\,t + x\,t^{-2} \right) \\ \left( 3\,x^2\,t^2 + t - 2\,x\,t^4 \right) \,\frac{\mathrm{d}x}{\mathrm{d}t} &= 2\,t^3 + 2\,x^2\,t^3 + x \\ \frac{\mathrm{d}x}{\mathrm{d}t} &= \frac{2\,t^3 + 2\,x^2\,t^3 + x}{3\,x^2\,t^2 + t - 2\,x\,t^4} \end{align*}$
Since we have this relationship between x and y, as the two sides are equal, so are their derivatives. We just have to remember that as y is a function of x, any function of y is also a function of x, with the inner function "y" composed inside whatever is being told to do to the y. So to differentiate these parts the Chain Rule would be needed. All other rules like the product and quotient rules will still apply as well. Anyway, differentiating both sides with respect to x gives
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x}\,\left( x\,y + x^2 \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left( y^2 \right) \\ x\,\frac{\mathrm{d}y}{\mathrm{d}x} + 1\,y + 2\,x &= \frac{\mathrm{d}y}{\mathrm{d}x}\,\frac{\mathrm{d}}{\mathrm{d}y}\,\left( y^2 \right) \\ x\,\frac{\mathrm{d}y}{\mathrm{d}x} + y + 2\,x &= \frac{\mathrm{d}y}{\mathrm{d}x}\,\left( 2\,y \right) \\ y + 2\,x &= 2\,y\,\frac{\mathrm{d}y}{\mathrm{d}x} - x\,\frac{\mathrm{d}y}{\mathrm{d}x} \\ y + 2\,x &= \left( 2\,y - x \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} \\ \frac{\mathrm{d}y}{\mathrm{d}x} &= \frac{y + 2\,x}{2\,y - x} \end{align*}$
This will be important for later. Going back a step and differentiating both sides with respect to x again we have
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}x} \,\left( y + 2\,x \right) &= \frac{\mathrm{d}}{\mathrm{d}x}\,\left[ \left( 2\,y - x \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} \right] \\ \frac{\mathrm{d}y}{\mathrm{d}x} + 2 &= \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} + \left( 2\,\frac{\mathrm{d}y}{\mathrm{d}x} - 1 \right) \,\frac{\mathrm{d}y}{\mathrm{d}x} \\ \frac{\mathrm{d}y}{\mathrm{d}x} + 2 &= \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} + 2\,\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 - \frac{\mathrm{d}y}{\mathrm{d}x} \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2 + 2\,\frac{\mathrm{d}y}{\mathrm{d}x} - 2\,\left( \frac{\mathrm{d}y}{\mathrm{d}x}\right) ^2 \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ 1 + \frac{\mathrm{d}y}{\mathrm{d}x} - \left( \frac{\mathrm{d}y}{\mathrm{d}x} \right) ^2 \right] \end{align*}$
and since we already found that $\displaystyle \begin{align*} \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{y + 2\,x}{2\,y - x } \end{align*}$ that means
$\displaystyle \begin{align*} \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2 \, \left[ 1 + \frac{y + 2\,x}{2\,y - x} - \left( \frac{y + 2\,x}{2\,y - x } \right) ^2 \right] \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ \frac{\left( 2\,y - x \right) ^2 + \left( 2\,y - x \right) \left( y + 2\,x \right) - \left( y + 2\,x \right) ^2}{\left( 2\,y - x \right) ^2 } \right] \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ \frac{4\,y^2 - 4\,x\,y + x^2 + 2\,y^2 + 4\,x\,y - x\,y - 2\,x^2 - y^2 - 4\,x\,y - 4\,x^2}{\left( 2\,y - x \right) ^2} \right] \\ \left( 2\,y - x \right) \,\frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= 2\,\left[ \frac{5\,y^2 - 5\,x\,y - 5\,x^2 }{\left( 2\,y - x \right) ^2} \right] \\ \frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} &= \frac{10\,\left( y^2 - x\,y - x^2 \right) }{\left( 2\,y - x \right) ^3} \end{align*}$View attachment 5526
Here x is a function of t, so again, to differentiate any x terms, we must use the Chain Rule.
$\displaystyle \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} \,\left( x^3 + x\,t^{-1} \right) &= \frac{\mathrm{d}}{\mathrm{d}t} \,\left[ t^2 \left( 1 + x^2 \right) \right] \\ \frac{\mathrm{d}x}{\mathrm{d}t} \, \frac{\mathrm{d}}{\mathrm{d}x} \, \left( x^3 \right) + \frac{\mathrm{d}x}{\mathrm{d}t} \, t^{-1} - x \, t^{-2} &= 2 \, t \, \left( 1 + x^2 \right) + t^2 \, \frac{ \mathrm{d}x }{ \mathrm{d}t } \, \frac{ \mathrm{d} }{\mathrm{d}x} \, \left( 1 + x^2 \right) \\ \frac{\mathrm{d}x}{\mathrm{d}t}\,\left( 3\,x^2 \right) + \frac{\mathrm{d}x}{\mathrm{d}t}\,t^{-1} - x \,t^{-2} &= 2\,t\,\left( 1 + x^2 \right) + t^2\,\frac{\mathrm{d}x}{\mathrm{d}t} \,\left( 2\,x \right) \\ 3\,x^2\,\frac{\mathrm{d}x}{\mathrm{d}t} + t^{-1}\,\frac{\mathrm{d}x}{\mathrm{d}t} - 2\,x\,t^2 \,\frac{\mathrm{d}x}{\mathrm{d}t} &= 2\,t + 2\,x^2\,t + x\,t^{-2} \\ t^2\,\left( 3\,x^2 + t^{-1} - 2\,x\,t^2 \right) \,\frac{\mathrm{d}x}{\mathrm{d}t} &= t^2\,\left( 2\,t + 2\,x^2\,t + x\,t^{-2} \right) \\ \left( 3\,x^2\,t^2 + t - 2\,x\,t^4 \right) \,\frac{\mathrm{d}x}{\mathrm{d}t} &= 2\,t^3 + 2\,x^2\,t^3 + x \\ \frac{\mathrm{d}x}{\mathrm{d}t} &= \frac{2\,t^3 + 2\,x^2\,t^3 + x}{3\,x^2\,t^2 + t - 2\,x\,t^4} \end{align*}$