MHB Keito's question at Yahoo Answers regarding the Law of Sines

[MarkFL]

Here is the question:

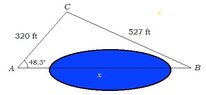
Points A and B are separated by a lake. To find the distance between them, a surveyor locates a point C on lan?

Points A and B are separated by a lake. To find the distance between them, a surveyor locates a point C on land such that angle CAB = 48.3°. He also measures CA as 320 ft and CB as 527 ft. Find the distance between A and B. (Round your answer to one decimal place.)

Thank you very much for the help!

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Keito,

First, let's draw a diagram:

View attachment 1381

We have let $x$, measured in ft, denote the distance between $A$ and $B$.

Using the Law of Sines, we may state:

$$\frac{\sin(B)}{320}=\frac{\sin\left(48.3^{\circ} \right)}{527}$$

Hence:

$$B=\sin^{-1}\left(\frac{320}{527}\sin\left(48.3^{\circ} \right) \right)$$

And so:

$$C=180^{\circ}-A-B=180^{\circ}-48.3^{\circ}-\sin^{-1}\left(\frac{320}{527}\sin\left(48.3^{\circ} \right) \right)=131.7^{\circ}-\sin^{-1}\left(\frac{320}{527}\sin\left(48.3^{\circ} \right) \right)$$

Rather than approximate this angle now, let's wait to round until the very last step. (Wink)

Now, using the Law of Sines again, we may state:

$$\frac{x}{\sin(C)}=\frac{527}{\sin\left(48.3^{\circ} \right)}$$

Hence:

$$x=\frac{527 \sin \left(131.7^{ \circ}- \sin^{-1} \left( \frac{320}{527} \sin \left(48.3^{ \circ} \right) \right) \right)}{ \sin \left(48.3^{ \circ} \right)} \approx682.6\text{ ft}$$