Kepler's 3rd Law, geometric relationship?

[Mr Joe Bangles]

Hello, quick question here

I am studying mathematical astronomy / the history of , and I have noted that by raising the average sidereal period of any planet in our solar system, to the power .666666, that you are left with the average distance of that planet from the Sun, in AU

I was told that this is essentially Kepler's 3rd law, restated, and that it was a " geometric relationship "

However, I am not a mathematician and don't understand how this

translates to this

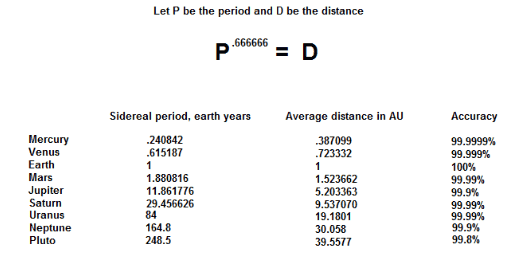Can somebody help clear this up for me ?

Thanks,
Joe

 

[Janus]

P^{0.666666...} = P^{\frac{2}{3}} = \sqrt[3]{P^2}

Kepler's law says:
The square of the period of any planet is proportional to the cube of the semimajor axis of its orbit. or

P^2 \propto D^3

 

[fresh_42]

Kepler's third law states: The squared orbit periods of two planets are proportional to the cubes of their semi-major axis.
That is
$$
\frac{P_1^2}{P_2^2}=\frac{a_1^3}{a_2^3} \textrm{ or } P^2 \sim a^3 \textrm{ or } P^{\frac{2}{3}}=P^{.66666} \sim a
$$
and your (and Kepler's) average distance $D=a$ is the length of the semi-major axis. The proportional factor is the Gaußian gravitational constant. For the derivation, see https://en.wikipedia.org/wiki/Specific_relative_angular_momentum.

 

[Mr Joe Bangles]

OK, thanks for putting it in traditional notation

That's very interesting, ...the cube root

The cube root of the ancients' 25,920 year equinox precession cycle is approximate to the synodic month average as per the Babylonian Zig Zag function

Perhaps a basis for associating the " Great Month " period to the lunisolar month average ?

Thanks,

Joe

 

[PeroK]

As you can see, a mittle laths goes a wong lay!

 

[Mr Joe Bangles]

Indeed, Perok.

This passage from Plato is what got me started on the topic, originally

"Now for divine begettings there is a period comprehended by a perfect number, and for mortal by the first in which augmentations dominating and dominated when they have attained to three distances and four limits of the assimilating and the dissimilating, the waxing and the waning, render all things conversable and commensurable [546c] with one another, whereof a basal four-thirds wedded to the pempad yields two harmonies at the third augmentation, the one the product of equal factors taken one hundred times, the other of equal length one way but oblong,-one dimension of a hundred numbers determined by the rational diameters of the pempad lacking one in each case, or of the irrational lacking two; the other dimension of a hundred cubes of the triad. And this entire geometrical number is determinative of this thing, of better and inferior births."

:)

Thanks, guys

Joe

 

[Evo]

You might not want to get too bogged down with ancient writings as far as being precise, as they have been vastly improved upon, to put it lightly.