wizzleman
- 5
- 0
Homework Statement
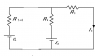
The circuit in the figure is composed of two batteries (ε1 = 9.0 V and ε2 = 5.0 V) and four resistors (R1 = 110.0 Ω, R2 = 40.0 Ω, R3 = 30.0 Ω, and R4 = 50.0 Ω) as shown.
1). What is the current I1 which flows through R1?
2). What is the current I3 which flows through R3?
Homework Equations
I used
ε1-R1I1+I2R2-R4I1-ε2=0
and
ε1-R1I1-R3I3-R4I1=0
The Attempt at a Solution
I've tried plugging in variables and attempting to solve for I3 but it's not the correct answer.