- #1
lodovico
- 17
- 0
circuit help -- resistors and batteries in a network
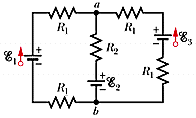
(a) Calculate the current through each ideal battery in Fig. 28-41.
(As a sign convention, assume the currents are "up" through each battery.)
A (I1)
A (I2)
A (I3)
Assume that R1 = 1.5 , R2 = 2.5 , ε1 = 2.0 V, and ε2 = ε3 = 3.5 V.
(b) Calculate Va - Vb
V=iR
I don't know how to approach this problem, use kirchhoffs law?
Homework Statement
(a) Calculate the current through each ideal battery in Fig. 28-41.
(As a sign convention, assume the currents are "up" through each battery.)
A (I1)
A (I2)
A (I3)
Assume that R1 = 1.5 , R2 = 2.5 , ε1 = 2.0 V, and ε2 = ε3 = 3.5 V.
(b) Calculate Va - Vb
Homework Equations
V=iR
The Attempt at a Solution
I don't know how to approach this problem, use kirchhoffs law?